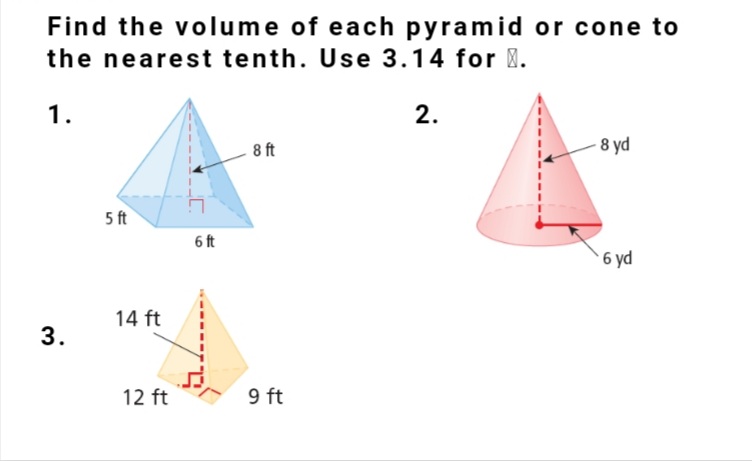
Find the volume of each pyramid or cone to the nearest tenth. Use 3.14 for π.

Steps to Solve

1. Volume of a Pyramid Formula The volume ( V ) of a pyramid is calculated using the formula: $$ V = \frac{1}{3} \times \text{Base Area} \times \text{Height} $$

For the pyramid in the first image, the base area is: Base area = base length × base width = ( 6 , \text{ft} \times 8 , \text{ft} = 48 , \text{ft}^2 )

Using the height of ( 5 , \text{ft} ): $$ V = \frac{1}{3} \times 48 , \text{ft}^2 \times 5 , \text{ft} $$

2. Calculate the Pyramid Volume Now calculate the volume: $$ V = \frac{1}{3} \times 48 \times 5 = \frac{240}{3} = 80 , \text{ft}^3 $$

3. Volume of a Cone Formula The volume ( V ) of a cone is calculated using the formula: $$ V = \frac{1}{3} \times \pi \times r^2 \times h $$ where ( r ) is the radius and ( h ) is the height.

For the second shape, the radius is half of the diameter, so: $$ r = \frac{8 , \text{yd}}{2} = 4 , \text{yd} $$

Using the height of ( 6 , \text{yd} ): $$ V = \frac{1}{3} \times 3.14 \times (4 , \text{yd})^2 \times 6 , \text{yd} $$

4. Calculate the Cone Volume Now calculate the volume: $$ V = \frac{1}{3} \times 3.14 \times 16 \times 6 = \frac{1}{3} \times 3.14 \times 96 = \frac{301.44}{3} \approx 100.5 , \text{yd}^3 $$

5. Volume of the Second Cone For the third shape, the radius is: $$ r = \frac{9 , \text{ft}}{2} = 4.5 , \text{ft} $$ Using the height of ( 14 , \text{ft} ): $$ V = \frac{1}{3} \times 3.14 \times (4.5 , \text{ft})^2 \times 14 , \text{ft} $$

6. Calculate the Second Cone Volume Now calculate the volume: $$ V = \frac{1}{3} \times 3.14 \times 20.25 \times 14 = \frac{1}{3} \times 3.14 \times 283.5 \approx \frac{889.89}{3} \approx 296.6 , \text{ft}^3 $$