Find the values of x for which log2 2x + log2 (x + 4) = 6.
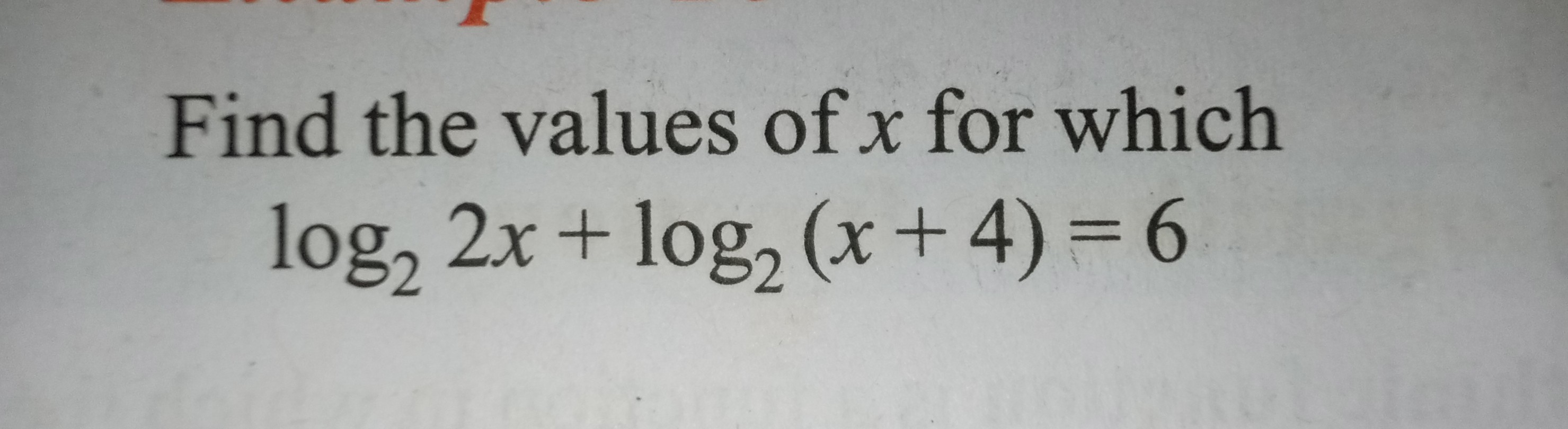
Understand the Problem
The question is asking to find the values of x that satisfy the equation involving logarithms. Specifically, it requires solving the equation log base 2 of 2x plus log base 2 of (x + 4) equals 6.
Answer
The solution is $x = 4$.
Answer for screen readers
The value of $x$ that satisfies the equation is $x = 4$.
Steps to Solve
- Combine Logarithmic Expressions
Use the property of logarithms that states $\log_a b + \log_a c = \log_a (bc)$.
So we can rewrite the equation as: $$\log_2 (2x) + \log_2 (x + 4) = \log_2 (2x(x + 4)).$$
The equation becomes: $$\log_2 (2x(x + 4)) = 6.$$
- Convert Logarithm to Exponential Form
To eliminate the logarithm, we convert the logarithmic equation to its exponential form: $$2^6 = 2x(x + 4).$$
Calculating $2^6$ gives us: $$64 = 2x(x + 4).$$
- Expand and Rearrange the Equation
Expanding the right side, we have: $$64 = 2x^2 + 8x.$$
To rearrange, set the equation to 0: $$2x^2 + 8x - 64 = 0.$$
- Divide through by 2
To simplify, divide the entire equation by 2: $$x^2 + 4x - 32 = 0.$$
- Factor the Quadratic Equation
Next, we will factor the quadratic expression: $$(x + 8)(x - 4) = 0.$$
- Solve for x
Setting each factor to zero gives us the solutions: $$x + 8 = 0 \quad \Rightarrow \quad x = -8,$$ $$x - 4 = 0 \quad \Rightarrow \quad x = 4.$$
- Check for Valid Solutions
Since logarithms are only defined for positive arguments, we check:
- For $x = -8$: $\log_2(2 \cdot -8)$ and $\log_2(-8 + 4)$ are not defined.
- For $x = 4$: Both $\log_2(2 \cdot 4)$ and $\log_2(4 + 4)$ are valid.
Thus, the only valid solution is $x = 4$.
The value of $x$ that satisfies the equation is $x = 4$.
More Information
This equation involves the properties of logarithms and quadratic equations. The base of the logarithm is 2, and the exponential form helps in transforming the equation to a more solvable format.
Tips
- Forgetting to check for the validity of solutions resulting from logarithmic equations.
- Misapplying logarithmic properties, such as incorrectly combining or expanding terms.
AI-generated content may contain errors. Please verify critical information