Find the values of P for which the matrix A = [[3, P, P], [P, 3, P], [P, P, 3]] is of rank 1.
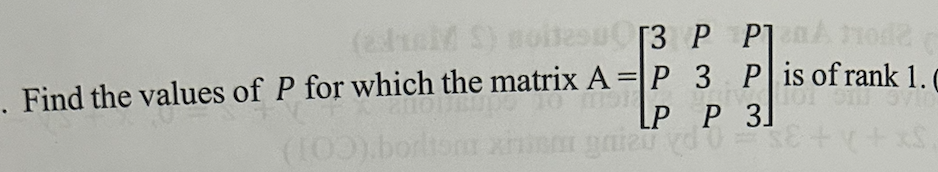
Understand the Problem
The question is asking for the values of P that make the given matrix A of rank 1. This involves understanding the properties of matrices and how their rank can be determined based on their elements.
Answer
The values of \( P \) are the roots of \( P^3 - 5P^2 + 27 = 0 \).
Answer for screen readers
The values of ( P ) for which the matrix ( A ) has rank 1 are the roots of the cubic equation ( P^3 - 5P^2 + 27 = 0 ). The roots can be approximated numerically, which generally will yield one real root and two complex roots.
Steps to Solve
-
Understand Rank of a Matrix The rank of a matrix is the maximum number of linearly independent rows or columns. For a matrix to have rank 1, all rows or all columns must be linearly dependent.
-
Set Up the Matrix Let's define the matrix ( A ): $$ A = \begin{bmatrix} 3 & P & P \ P & 3 & P \ P & P & 3 \end{bmatrix} $$
-
Calculate the Determinant For ( A ) to have rank 1, its determinant must be zero. We calculate the determinant: $$ \text{det}(A) = 3(3(3) - P^2) - P(P(3) - P^2) + P(P^2 - 3P) $$ This simplifies to: $$ \text{det}(A) = 27 - 3P^2 - (3P^2 - P^3) + (P^3 - 3P^2) $$ Therefore: $$ \text{det}(A) = 27 - 5P^2 + P^3 $$
-
Set the Determinant to Zero To find the values of ( P ) for which ( A ) has rank 1, we set the determinant to zero: $$ P^3 - 5P^2 + 27 = 0 $$
-
Solve the Cubic Equation We can use methods such as synthetic division, factoring, or numerical methods to find the roots of the equation ( P^3 - 5P^2 + 27 = 0 ). This may not factor easily, so we can check for rational roots or use numerical methods.
The values of ( P ) for which the matrix ( A ) has rank 1 are the roots of the cubic equation ( P^3 - 5P^2 + 27 = 0 ). The roots can be approximated numerically, which generally will yield one real root and two complex roots.
More Information
The rank of a matrix gives insights into the solutions of linear systems associated with the matrix. A rank of 1 indicates that any two rows or columns are scalar multiples of each other.
Tips
- Forgetting to set the determinant equal to zero is a common error when determining conditions for the rank.
- Incorrectly simplifying the determinant can lead to wrong roots.
- Misidentifying the nature (real vs. complex) of the roots when solving cubic equations.
AI-generated content may contain errors. Please verify critical information