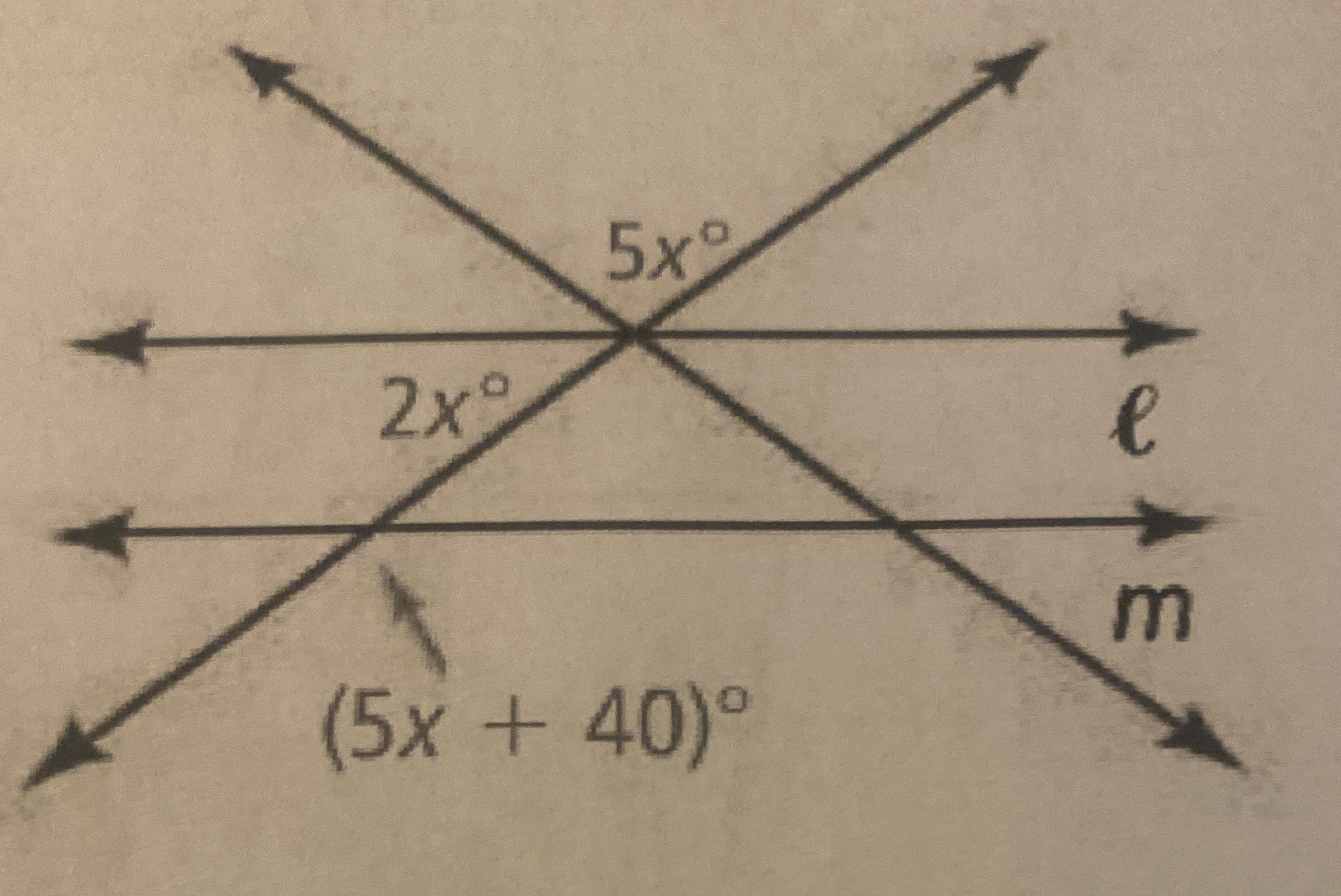
Find the value of x given the angles 2x°, 5x°, and (5x + 40)° formed by two intersecting lines.
Understand the Problem
The question involves finding the value of 'x' in an equation based on the angles formed by two intersecting lines. Specifically, it identifies relationships among these angles, which can be used to set up an equation for solving 'x'.
Answer
The value of \( x \) is \( 20 \).
Answer for screen readers
The value of ( x ) is ( 20 ).
Steps to Solve
-
Identify the Relationships Between Angles The diagram shows two intersecting lines creating several angles. According to the properties of vertically opposite angles, we know that angles across from one another are equal. We can set up the following equation from the given angles: $$ 2x = 5x $$
-
Set Up the Equation We also see another angle described as $(5x + 40)^\circ$, which is adjacent to the angle $2x^\circ$. The sum of these two angles should equal $180^\circ$. Therefore: $$ 2x + (5x + 40) = 180 $$
-
Combine Like Terms Combine the terms in the equation: $$ 2x + 5x + 40 = 180 $$
-
Simplify the Equation This simplifies to: $$ 7x + 40 = 180 $$
-
Isolate x Now, to solve for $x$, we first subtract $40$ from both sides: $$ 7x = 180 - 40 $$ $$ 7x = 140 $$
-
Divide by the Coefficient Next, divide both sides by $7$: $$ x = \frac{140}{7} $$ $$ x = 20 $$
The value of ( x ) is ( 20 ).
More Information
In this problem, we used the properties of angles formed by intersecting lines. Vertically opposite angles are equal, and adjacent angles on a straight line sum to ( 180^\circ ), which helped set up the equation needed to solve for ( x ).
Tips
- Ignoring Adjacent Angle Properties: Some may forget that adjacent angles on a straight line sum up to ( 180^\circ ), leading to incorrect equations.
- Incorrectly Combining Like Terms: Ensure that all terms are correctly combined when simplifying equations.
AI-generated content may contain errors. Please verify critical information