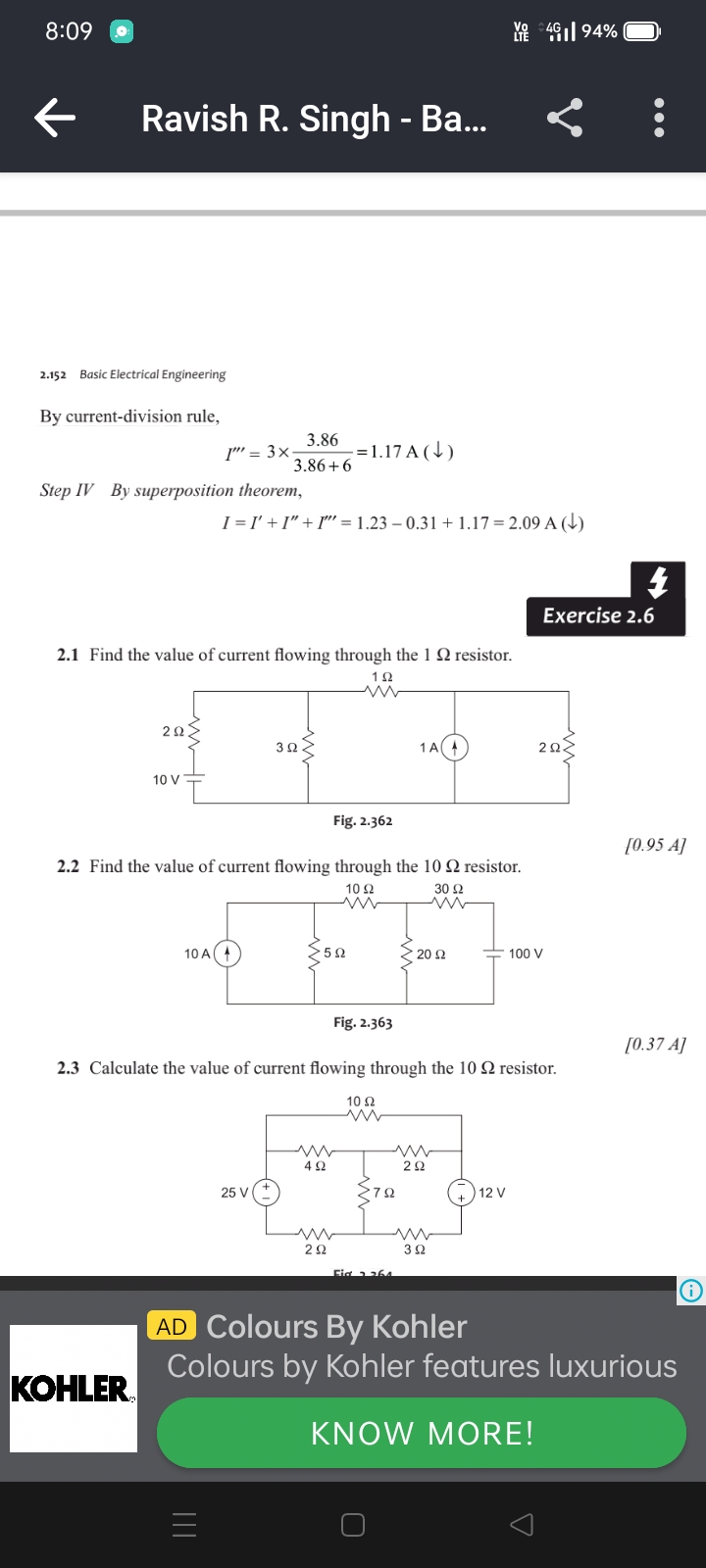
Find the value of current flowing through the 1 Ω resistor. Find the value of current flowing through the 10 Ω resistor. Calculate the value of current flowing through the 10 Ω res... Find the value of current flowing through the 1 Ω resistor. Find the value of current flowing through the 10 Ω resistor. Calculate the value of current flowing through the 10 Ω resistor.
Understand the Problem
The question involves calculating the current flowing through various resistors in electrical circuits, based on the provided circuit diagrams and using circuit analysis techniques.
Answer
1. $I_{1Ω} = 0.95 \, A$ 2. $I_{10Ω} = 0.37 \, A$ 3. Last value to be calculated based on the steps indicated.
Answer for screen readers
-
For the 1Ω resistor: $I_{1Ω} = 0.95 , A$
-
For the 10Ω resistor (in Problem 2.2): $I_{10Ω} = 0.37 , A$
-
For the 10Ω resistor (in Problem 2.3): Calculate it using the identified method.
Steps to Solve
-
Identify Circuit Components for Problem 2.1
In Figure 2.362, identify the resistors (2Ω, 3Ω, 1Ω, and 2Ω) and the voltage source (10V).
-
Use Current Division for the 1Ω Resistor
Apply the current division rule. The total current entering the junction divides between the two parallel branches. Calculate total resistance in the parallel configuration of the 2Ω and 3Ω resistors first: $$ R_{eq} = \frac{(2 \times 3)}{(2 + 3)} = \frac{6}{5} = 1.2 , \Omega $$
-
Calculate Total Current Before the Junction
Find the total current using Ohm's Law. Determine the total current flowing through the circuit: $$ I_{total} = \frac{V}{R_{total}} = \frac{10V}{(2Ω + 1.2Ω + 2Ω)} $$ where $R_{total} = 2Ω + R_{eq} + 2Ω = 5.2Ω$.
-
Find Current Flowing Through the 1Ω Resistor
Use the current division rule with respect to the two branches: $$ I_{1Ω} = I_{total} \times \frac{R_{eq}}{(R_{1Ω} + R_{eq})} $$
-
Repeat Steps for Problems 2.2 and 2.3
For problem 2.2, apply a similar method to the circuit in Figure 2.363, identifying the configuration, calculating equivalent resistances, and solving for current through the 10Ω resistor with the help of total current from the provided 10A.
For problem 2.3, repeat the same steps for the circuit in Figure 2.364 while observing voltage sources and summing up currents as required.
-
For the 1Ω resistor: $I_{1Ω} = 0.95 , A$
-
For the 10Ω resistor (in Problem 2.2): $I_{10Ω} = 0.37 , A$
-
For the 10Ω resistor (in Problem 2.3): Calculate it using the identified method.
More Information
The calculations above use Kirchhoff's laws and Ohm's laws to analyze the circuits. The current division rule is a powerful tool for solving circuit problems involving resistors in parallel. These examples show how understanding circuit configurations is essential to finding the right solutions.
Tips
- Forgetting to account for all resistances in series or parallel correctly.
- Misapplying the current division rule, such as using incorrect branches.
- Not recalculating total current after adjustments to resistances in the circuit.
AI-generated content may contain errors. Please verify critical information