Find the value of $16^{-\frac{3}{2}}$.
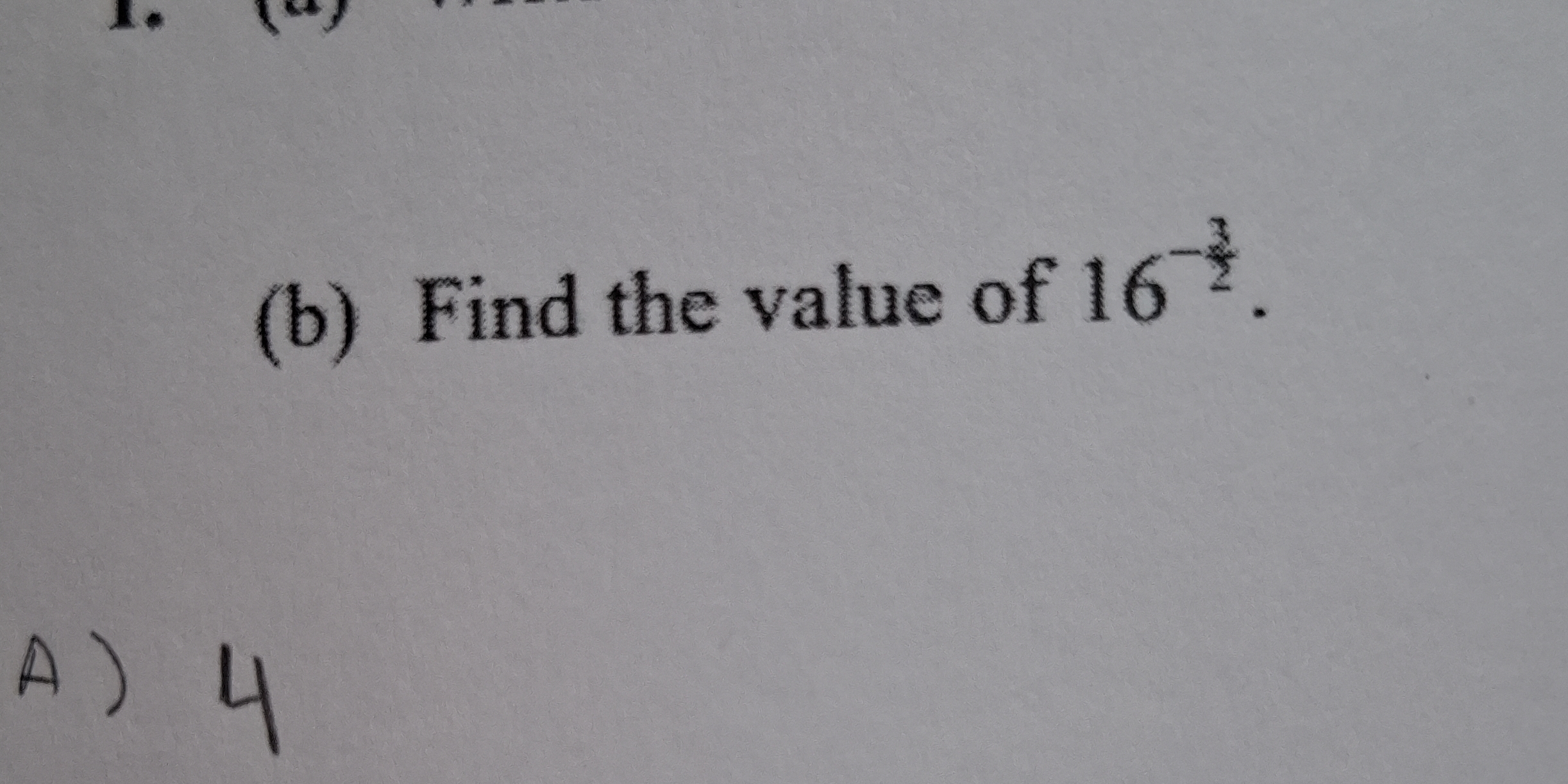
Understand the Problem
The question asks to find the value of 16 raised to the power of -3/2. This involves understanding fractional exponents and negative exponents.
Answer
$\frac{1}{64}$
Answer for screen readers
$\frac{1}{64}$
Steps to Solve
- Rewrite with a positive exponent A negative exponent means we take the reciprocal of the base raised to the positive exponent.
$16^{-\frac{3}{2}} = \frac{1}{16^{\frac{3}{2}}}$
- Express the fractional exponent as a radical and a power The denominator of the fractional exponent is the index of the radical, and the numerator is the power.
$\frac{1}{16^{\frac{3}{2}}} = \frac{1}{(\sqrt{16})^3}$
- Evaluate the square root
$\sqrt{16} = 4$
$\frac{1}{(\sqrt{16})^3} = \frac{1}{4^3}$
- Evaluate the cube
$4^3 = 4 \cdot 4 \cdot 4 = 64$
$\frac{1}{4^3} = \frac{1}{64}$
$\frac{1}{64}$
More Information
$16^{-\frac{3}{2}}$ can also be interpreted as $(\sqrt{16})^{-3}$.
Tips
A common mistake is to apply the negative exponent only to the numerator or denominator of the fractional exponent, instead of applying it to the entire base. Another error is incorrectly calculating the square root or the cube.
AI-generated content may contain errors. Please verify critical information