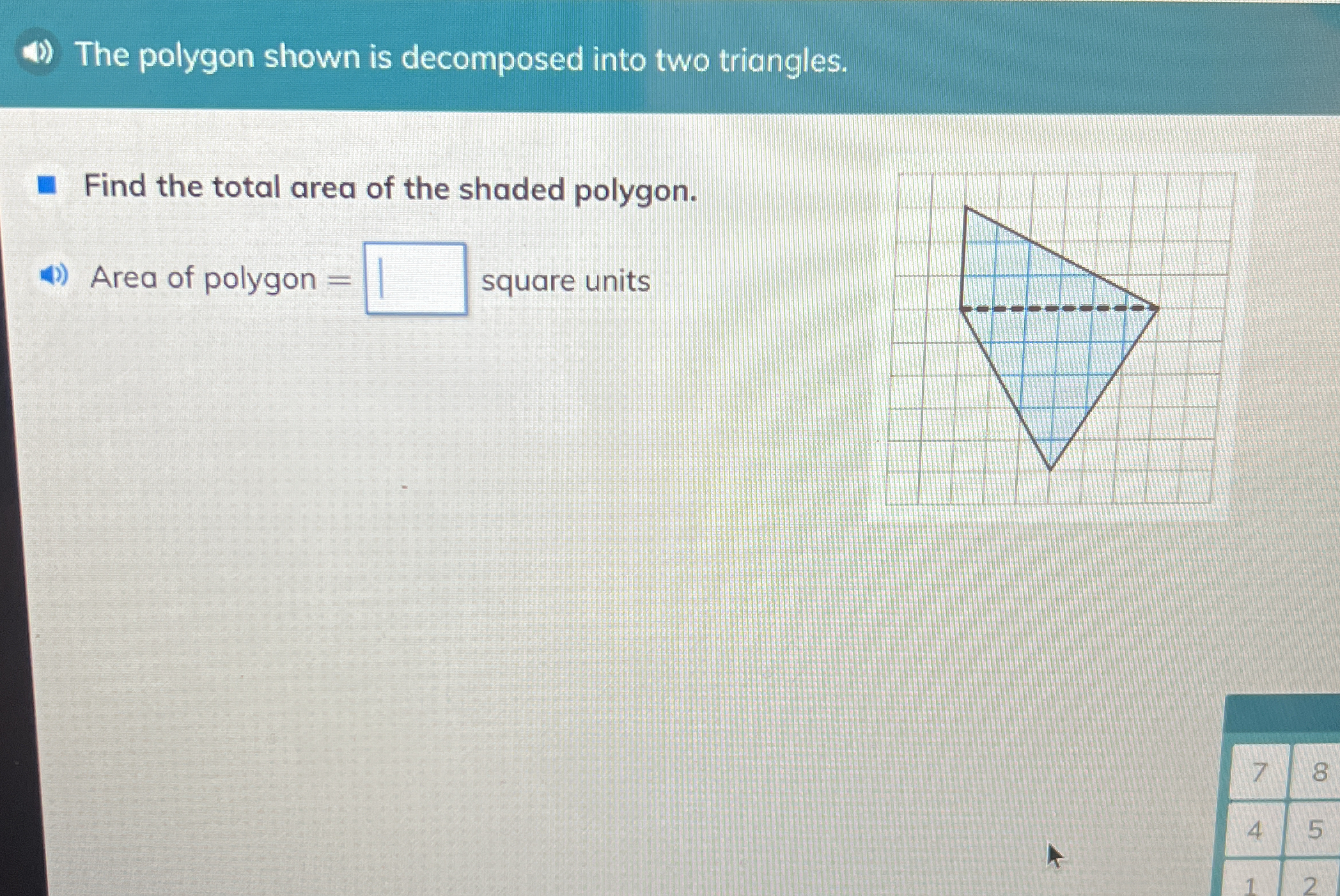
Find the total area of the shaded polygon.
Understand the Problem
The question is asking to calculate the total area of a shaded polygon that is composed of two triangles. To solve it, we will need to use the properties of triangles and possibly the grid provided to find the dimensions necessary for calculating the area.
Answer
The area of the polygon is $5$ square units.
Answer for screen readers
The area of the polygon is equal to 5 square units.
Steps to Solve
- Identify the triangles in the polygon
The shaded polygon consists of two triangles. We need to analyze the vertices and dimensions of each triangle based on the grid.
- Calculate the area of the first triangle
Using the formula for the area of a triangle:
$$ \text{Area} = \frac{1}{2} \times \text{base} \times \text{height} $$
Assuming the first triangle has a base of 3 units and height of 2 units (based on the grid), we calculate:
$$ \text{Area}_1 = \frac{1}{2} \times 3 \times 2 = 3 $$
- Calculate the area of the second triangle
Similarly, examine the second triangle. Assuming it has a base of 2 units and height of 2 units, we calculate:
$$ \text{Area}_2 = \frac{1}{2} \times 2 \times 2 = 2 $$
- Add the areas of both triangles
Now that we have the areas, sum them up:
$$ \text{Total Area} = \text{Area}_1 + \text{Area}_2 = 3 + 2 = 5 $$
The area of the polygon is equal to 5 square units.
More Information
The area is calculated by breaking the polygon into two triangles and applying the triangle area formula. This method is useful in geometry for calculating areas of complex shapes.
Tips
One common mistake is incorrectly identifying the base and height of the triangles. Always ensure you're measuring the dimensions correctly according to the grid lines.
AI-generated content may contain errors. Please verify critical information