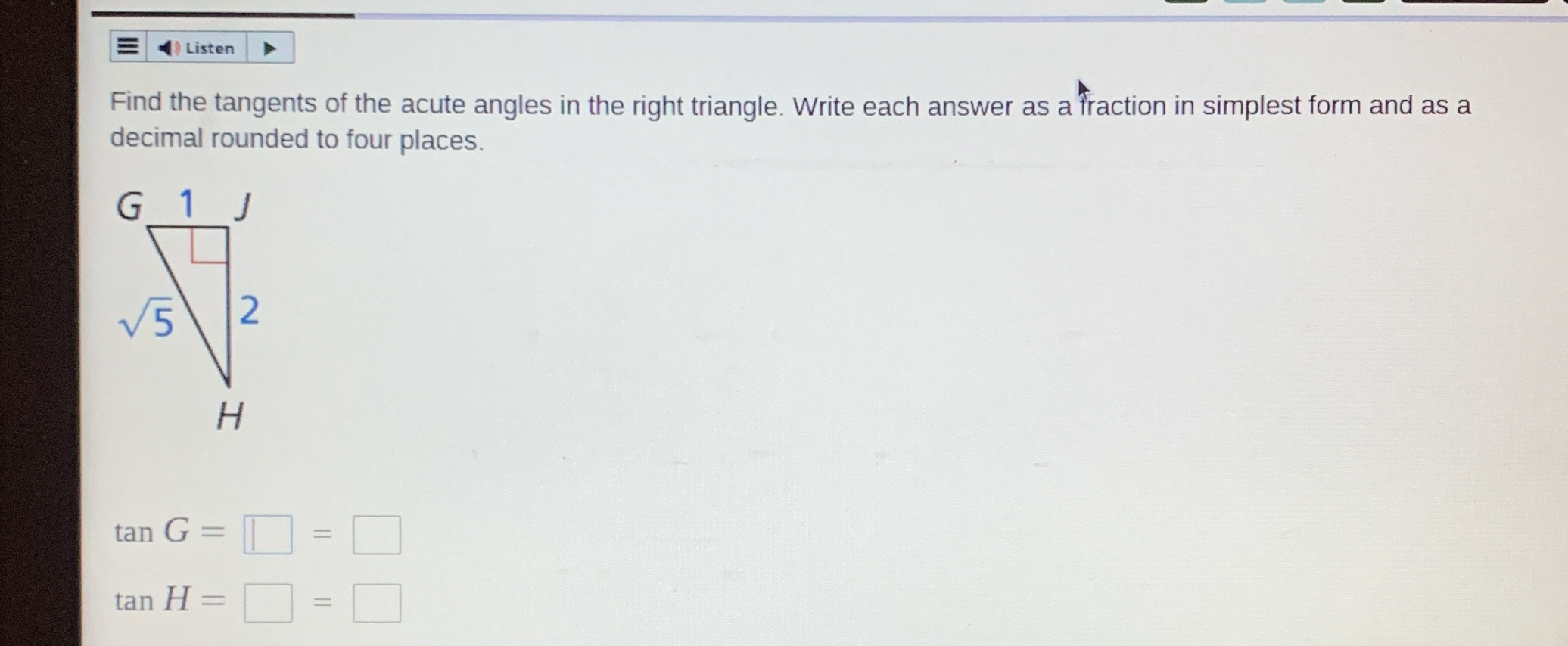
Find the tangents of the acute angles in the right triangle. Write each answer as a fraction in simplest form and as a decimal rounded to four places.

Steps to Solve

1. Identify the triangle sides The sides of the triangle are labeled as follows:

• Opposite side to angle ( G ) is ( 1 )
• Adjacent side to angle ( G ) is ( \sqrt{5} )
• The hypotenuse is ( 2 )

2. Find the tangent of angle ( G ) The tangent of an angle in a right triangle is defined as the ratio of the opposite side to the adjacent side. For angle ( G ): $$ \tan(G) = \frac{\text{Opposite}}{\text{Adjacent}} = \frac{1}{\sqrt{5}} $$

3. Simplify the tangent of angle ( G ) To express the tangent in simplest form, multiply the numerator and the denominator by ( \sqrt{5} ): $$ \tan(G) = \frac{1}{\sqrt{5}} \cdot \frac{\sqrt{5}}{\sqrt{5}} = \frac{\sqrt{5}}{5} $$

4. Calculate decimal value for ( \tan(G) ) To get the decimal value of ( \tan(G) ): $$ \tan(G) \approx \frac{\sqrt{5}}{5} \approx 0.4472 $$ (rounded to four decimal places)

5. Find the tangent of angle ( H ) For angle ( H ), the opposite side is ( \sqrt{5} ) and the adjacent side is ( 1 ): $$ \tan(H) = \frac{\text{Opposite}}{\text{Adjacent}} = \frac{\sqrt{5}}{1} = \sqrt{5} $$

6. Calculate decimal value for ( \tan(H) ) To find the decimal value of ( \tan(H) ): $$ \tan(H) \approx 2.2361 $$ (rounded to four decimal places)