Find the solution of the system of equations: -8x + 7y = -2 and -8x + 8y = 8.
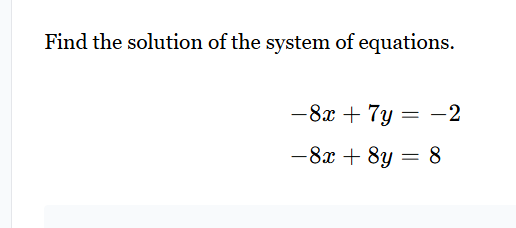
Understand the Problem
The question is asking to find the solution to a system of two equations involving the variables x and y. The system provided consists of two linear equations, which can be solved using methods such as substitution or elimination.
Answer
The solution is \( (x, y) = (9, 10) \).
Answer for screen readers
The solution to the system of equations is ( x = 9 ) and ( y = 10 ).
Steps to Solve
-
Label the Equations Let the first equation be Equation (1): $$ -8x + 7y = -2 $$ Let the second equation be Equation (2): $$ -8x + 8y = 8 $$
-
Eliminate x by Subtracting the Equations We subtract Equation (1) from Equation (2) to eliminate $x$: $$ (-8x + 8y) - (-8x + 7y) = 8 - (-2) $$ This simplifies to: $$ y = 10 $$
-
Substitute y Back into One of the Original Equations Now substitute $y = 10$ into either Equation (1) or Equation (2). Let's use Equation (1): $$ -8x + 7(10) = -2 $$ Simplifying gives: $$ -8x + 70 = -2 $$
-
Solve for x Rearranging the equation to solve for $x$: $$ -8x = -2 - 70 $$ $$ -8x = -72 $$ Now divide both sides by -8: $$ x = 9 $$
The solution to the system of equations is ( x = 9 ) and ( y = 10 ).
More Information
The solution represents the point where the two lines defined by the equations intersect. This means that both equations hold true at the values ( x = 9 ) and ( y = 10 ). The system had a unique solution because the two lines are not parallel.
Tips
- Neglecting Signs: Be careful with negative signs when rewriting equations or performing arithmetic operations. Always double-check calculations after each step.
- Wrong Substitution: Ensure that when substituting back to solve for one variable, you're using the correct equation and order of operations.
AI-generated content may contain errors. Please verify critical information