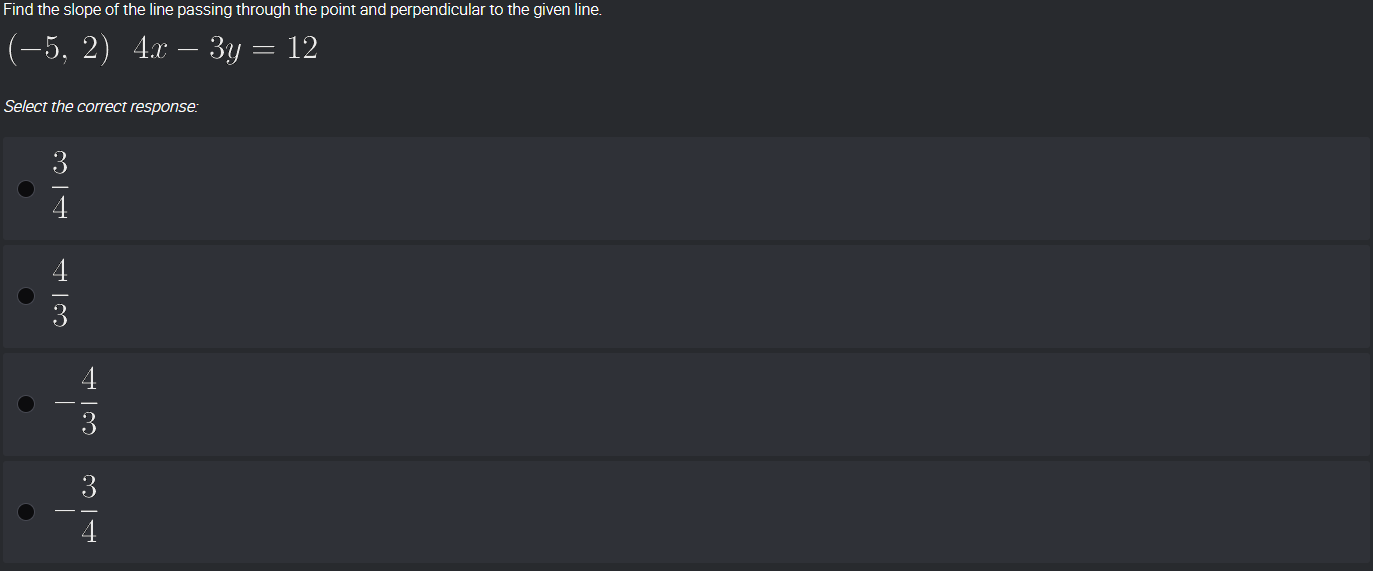
Find the slope of the line passing through the point (-5, 2) and perpendicular to the given line 4x - 3y = 12.
Understand the Problem
The question is asking to find the slope of a line that passes through a specific point and is perpendicular to the given line represented by the equation 4x - 3y = 12. To solve this, we need to first determine the slope of the given line, and then find the negative reciprocal of that slope for the perpendicular line.
Answer
The slope of the line is $-\frac{3}{4}$.
Answer for screen readers
The slope of the line is $-\frac{3}{4}$.
Steps to Solve
- Convert the line equation to slope-intercept form
To find the slope of the line given by the equation $4x - 3y = 12$, let's solve for $y$:
$$ -3y = -4x + 12 $$
Now, divide by -3:
$$ y = \frac{4}{3}x - 4 $$
Thus, the slope ($m_1$) of the given line is $\frac{4}{3}$.
- Find the slope of the perpendicular line
The slope of a line perpendicular to another is the negative reciprocal of the original slope. Therefore, if the slope of the original line is $m_1 = \frac{4}{3}$, the slope of the perpendicular line ($m_2$) is:
$$ m_2 = -\frac{1}{m_1} = -\frac{1}{\frac{4}{3}} = -\frac{3}{4} $$
- Final answer
The slope of the line passing through the point $(-5, 2)$ and perpendicular to the given line is $-\frac{3}{4}$.
The slope of the line is $-\frac{3}{4}$.
More Information
The relationship between the slopes of two perpendicular lines is an important concept in geometry. If one line has a slope of $\frac{a}{b}$, then a line perpendicular to it will have a slope of $-\frac{b}{a}$. This property is useful in various applications, including engineering and physics.
Tips
- Forgetting to take the negative reciprocal of the slope.
- Misplacing the negative sign, especially when converting to perpendicular slopes.
AI-generated content may contain errors. Please verify critical information