Find the quadratic equation with the root (α²,B) = 3 and α - β = 2.
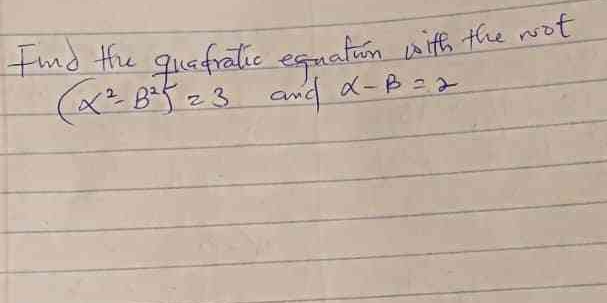
Understand the Problem
The question is asking to find a quadratic equation given that one of the roots is expressed in terms of variables and relationships between those variables. This involves using the relationships between roots and coefficients to formulate the quadratic equation.
Answer
The quadratic equation is: $$ x^2 - (2\alpha - 2)x + (\alpha^2 - 2\alpha) = 0 $$
Answer for screen readers
The quadratic equation is:
$$ x^2 - (2\alpha - 2)x + (\alpha^2 - 2\alpha) = 0 $$
Steps to Solve
- Identify the given information
We have a root $(\alpha^2, B) = 3$, which means $\alpha^2 + B = 3$. Additionally, we know that $\alpha - \beta = 2$.
- Express B in terms of α
From the first equation, we can isolate $B$: $$ B = 3 - \alpha^2 $$
- Express β in terms of α
Using the second equation, we can express $\beta$ in terms of $\alpha$: $$ \beta = \alpha - 2 $$
- Sum and Product of Roots
The roots of a quadratic equation can be denoted as $\alpha$ and $\beta$. The sum of the roots is given by: $$ \text{Sum} = \alpha + \beta $$ Replacing $\beta$: $$ \text{Sum} = \alpha + (\alpha - 2) = 2\alpha - 2 $$
The product of the roots is given by: $$ \text{Product} = \alpha \cdot \beta = \alpha(\alpha - 2) = \alpha^2 - 2\alpha $$
- Form the quadratic equation
Using the standard form of a quadratic equation $x^2 - (\text{Sum})x + \text{Product} = 0$: $$ x^2 - (2\alpha - 2)x + (\alpha^2 - 2\alpha) = 0 $$
- Final simplification
Simplifying the quadratic equation yields: $$ x^2 - (2\alpha - 2)x + (\alpha^2 - 2\alpha) = 0 $$
This is the quadratic equation formed using the roots based on the given conditions.
The quadratic equation is:
$$ x^2 - (2\alpha - 2)x + (\alpha^2 - 2\alpha) = 0 $$
More Information
This quadratic equation expresses the relationship between the roots $\alpha$ and $\beta$ while incorporating the conditions provided in the problem. Quadratic equations are foundational in algebra and are pivotal in various applications such as physics and engineering.
Tips
- Confusing the order of the roots: Ensure you maintain the correct relationships when substituting values.
- Miscalculating the sum or product of roots: Double-check the computations for accuracy, particularly when manipulating the equations.
- Forgetting to simplify: Always simplify expressions to their lowest terms for clarity.
AI-generated content may contain errors. Please verify critical information