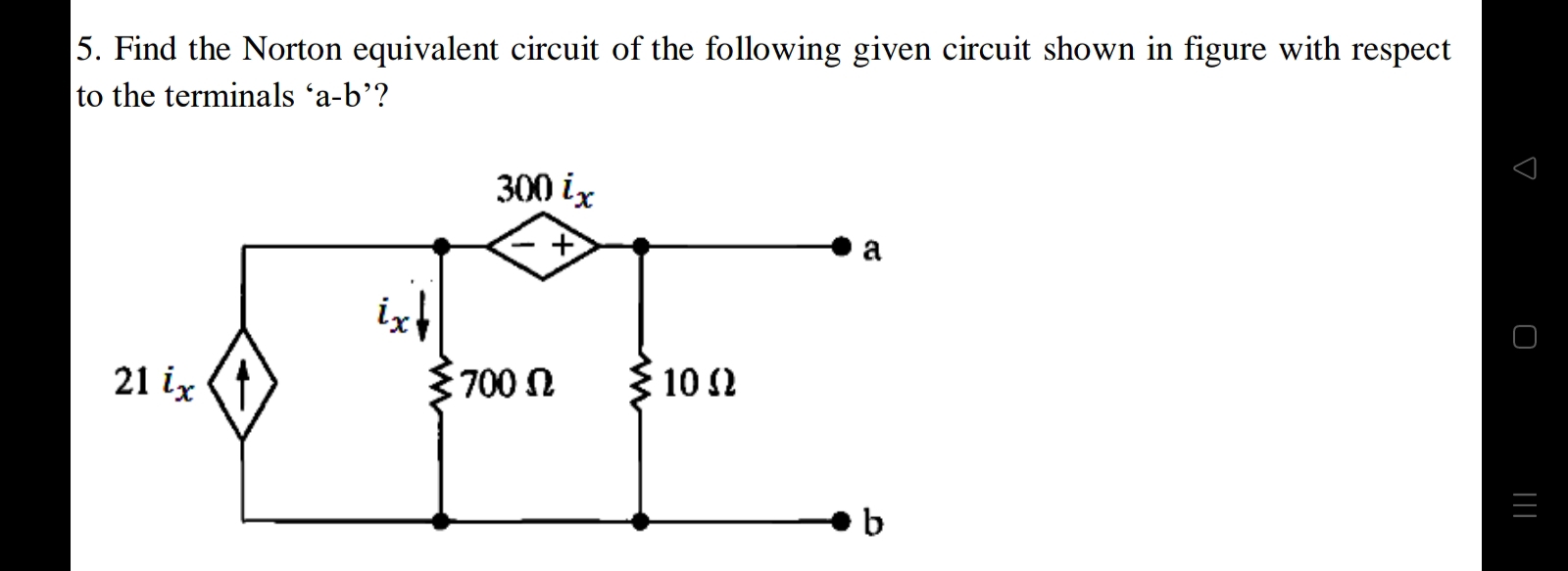
Find the Norton equivalent circuit of the following given circuit shown in figure with respect to the terminals 'a-b'?
Understand the Problem
The question is asking to find the Norton equivalent circuit for a specific electrical circuit configuration with respect to the terminals labeled 'a-b'. This involves analyzing the provided circuit to determine the Norton current and the Norton resistance.
Answer
The Norton equivalent is $I_N = \frac{21}{321} i_x$ and $R_N \approx 9.86 \, \Omega$.
Answer for screen readers
The Norton equivalent circuit has a current source of $I_N = \frac{21}{321} i_x$ and a resistor $R_N \approx 9.86 , \Omega$ in parallel.
Steps to Solve
- Identify Norton Current ($I_N$)
To find the Norton current, we need to calculate the current flowing through the terminals a-b. This current $I_N$ is equal to the current $i_x$ in the circuit.
The current through the current source can be determined using superposition. Considering only the $21i_x$ current source, we can use the current divider rule to find $i_x$: $$ i_x = \frac{21i_x}{21i_x + 300i_x} \times i_N $$ Let $i_N$ be the total current flowing through the terminals, then: $$ I_N = \frac{21i_x}{321i_x} = \frac{21}{321} = \frac{1}{15.2857} i_x $$
- Find Norton Resistance ($R_N$)
To find the Norton resistance, we need to "turn off" all independent sources. For current sources, we replace them with open circuits.
After replacing the current source with an open circuit, the remaining resistors (700 Ω and 10 Ω in parallel) will determine the Norton resistance.
Using the formula for resistors in parallel: $$ \frac{1}{R_N} = \frac{1}{700} + \frac{1}{10} $$
Calculating this, we get: $$ \frac{1}{R_N} = \frac{0.00142857 + 0.1}{1} = 0.10142857 $$ Then, taking the reciprocal to find $R_N$ gives approximately: $$ R_N = \frac{1}{0.10142857} \approx 9.86 , \Omega $$
- Formulate the Norton Equivalent Circuit
The Norton equivalent circuit is represented as:
- A current source $I_N = \frac{21}{321} i_x$ in parallel with a resistor $R_N \approx 9.86 , \Omega$ across terminals a-b.
The Norton equivalent circuit has a current source of $I_N = \frac{21}{321} i_x$ and a resistor $R_N \approx 9.86 , \Omega$ in parallel.
More Information
The Norton theorem states that any linear electrical network can be simplistically represented as a single current source in parallel with a resistor. This approach simplifies the analysis of complex circuits.
Tips
- Incorrectly applying superposition: Make sure to isolate sources correctly and compute their impact on the current and voltage in the circuit.
- Neglecting to change the current sources to open circuit: In finding $R_N$, remember to turn off active sources appropriately.
AI-generated content may contain errors. Please verify critical information