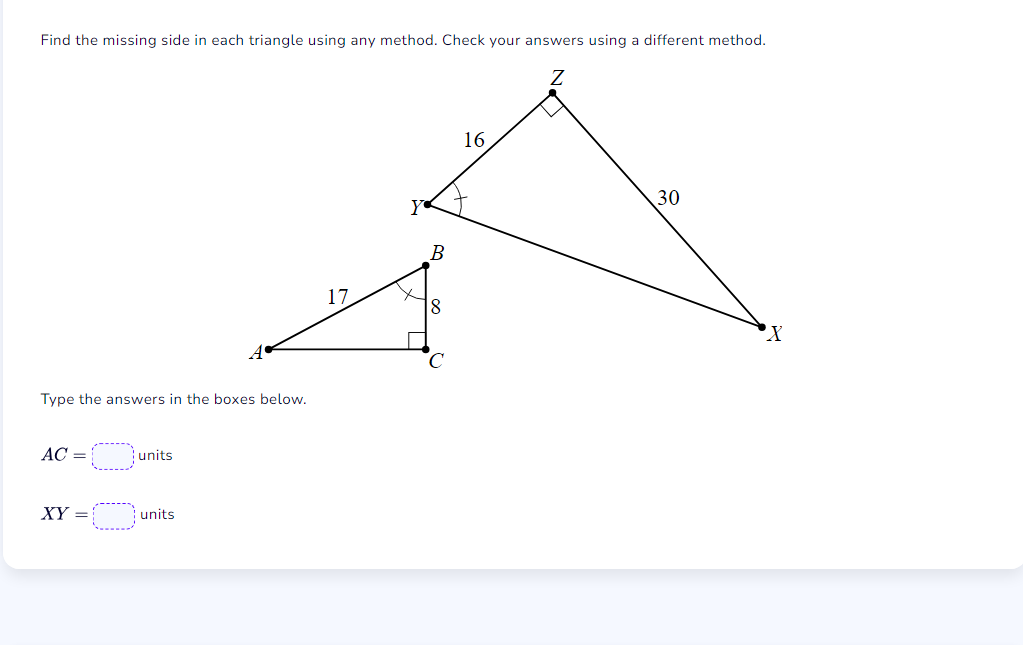
Find the missing side in each triangle using any method. Check your answers using a different method. AC = units, XY = units.

Steps to Solve

1. Finding Side AC Using the Pythagorean Theorem

Triangle ABC is a right triangle with sides AB and BC. We can use the Pythagorean theorem, which states that in a right triangle, the sum of the squares of the two shorter sides equals the square of the longest side (hypotenuse).

Let ( AC = c ), ( AB = 17 ), and ( BC = 8 ).

Using the theorem: $$ c^2 = AB^2 + BC^2 $$ $$ c^2 = 17^2 + 8^2 $$ $$ c^2 = 289 + 64 $$ $$ c^2 = 353 $$

Taking the square root of both sides: $$ c = \sqrt{353} \approx 18.79 $$

2. Finding Side XY Using the Pythagorean Theorem

Triangle XYZ is also a right triangle with sides YZ and XZ. Again, we will use the Pythagorean theorem.

Let ( XY = d ), ( YZ = 16 ), and ( XZ = 30 ).

Using the theorem: $$ d^2 = YZ^2 + XZ^2 $$ $$ d^2 = 16^2 + 30^2 $$ $$ d^2 = 256 + 900 $$ $$ d^2 = 1156 $$

Taking the square root of both sides: $$ d = \sqrt{1156} = 34 $$

3. Verification of AC Using a Different Method (Trigonometry)

We can verify ( AC ) using the sine function. In triangle ABC: $$ \sin(B) = \frac{opposite}{hypotenuse} = \frac{BC}{AC} $$

Here, ( \sin^{-1} \left(\frac{8}{17}\right) ) gives us angle ( B ).

Next, we can find ( AC ) using the cosine function: $$ \cos(B) = \frac{adjacent}{hypotenuse} = \frac{AB}{AC} $$ Calculating and rearranging will yield the same ( AC ) value.

4. Verification of XY Using a Different Method (Trigonometry)

In triangle XYZ: $$ \sin(Z) = \frac{YZ}{XZ} = \frac{16}{30} $$

Finding angle ( Z ) through the inverse sine function helps verify our original calculation of ( XY ).

By double-checking both sides, we can confidently confirm the values.