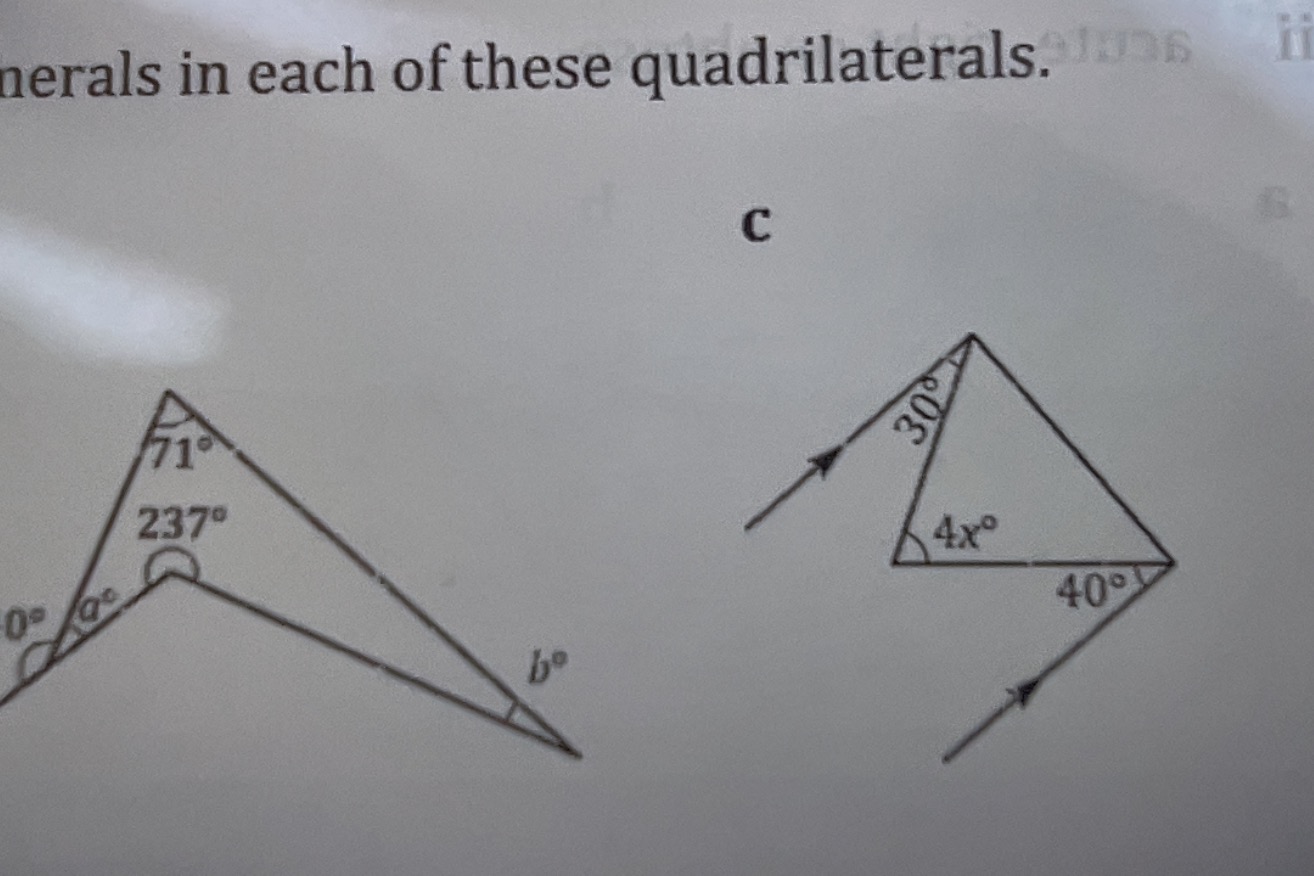
Find the missing angles in each of these quadrilaterals.

Steps to Solve

1. Identify Quadrilateral Properties

The sum of the angles in a quadrilateral is always $360^\circ$. In both quadrilaterals, we will apply this property.

2. First Quadrilateral Calculation

For the first quadrilateral, we have angles $0^\circ$, $71^\circ$, and $237^\circ$.

Using the formula for the sum of angles:

$$ 0^\circ + 71^\circ + 237^\circ + a^\circ = 360^\circ $$

3. Solve for the Unknown Angle ( a )

Rearranging the equation:

$$ a^\circ = 360^\circ - (71^\circ + 237^\circ) $$

Calculating the right side:

$$ a^\circ = 360^\circ - 308^\circ = 52^\circ $$

Thus, ( a = 52^\circ ).

4. Second Quadrilateral Calculation

For the second quadrilateral, we have angles $30^\circ$, $40^\circ$, and $4x^\circ$.

Again, applying the property of quadrilaterals:

$$ 30^\circ + 40^\circ + 4x^\circ + 30^\circ = 360^\circ $$

5. Combine Like Terms

Simplifying the equation:

$$ 100^\circ + 4x^\circ = 360^\circ $$

6. Solve for the Unknown ( x )

Rearranging gives:

$$ 4x^\circ = 360^\circ - 100^\circ $$

Calculating:

$$ 4x^\circ = 260^\circ $$

Dividing by 4:

$$ x = \frac{260^\circ}{4} = 65^\circ $$

7. Final Angle Calculation

To get ( 4x^\circ ):

$$ 4x^\circ = 4 \times 65^\circ = 260^\circ $$

Thus, the angles are ( 30^\circ, 40^\circ, \text{ and } 260^\circ ).