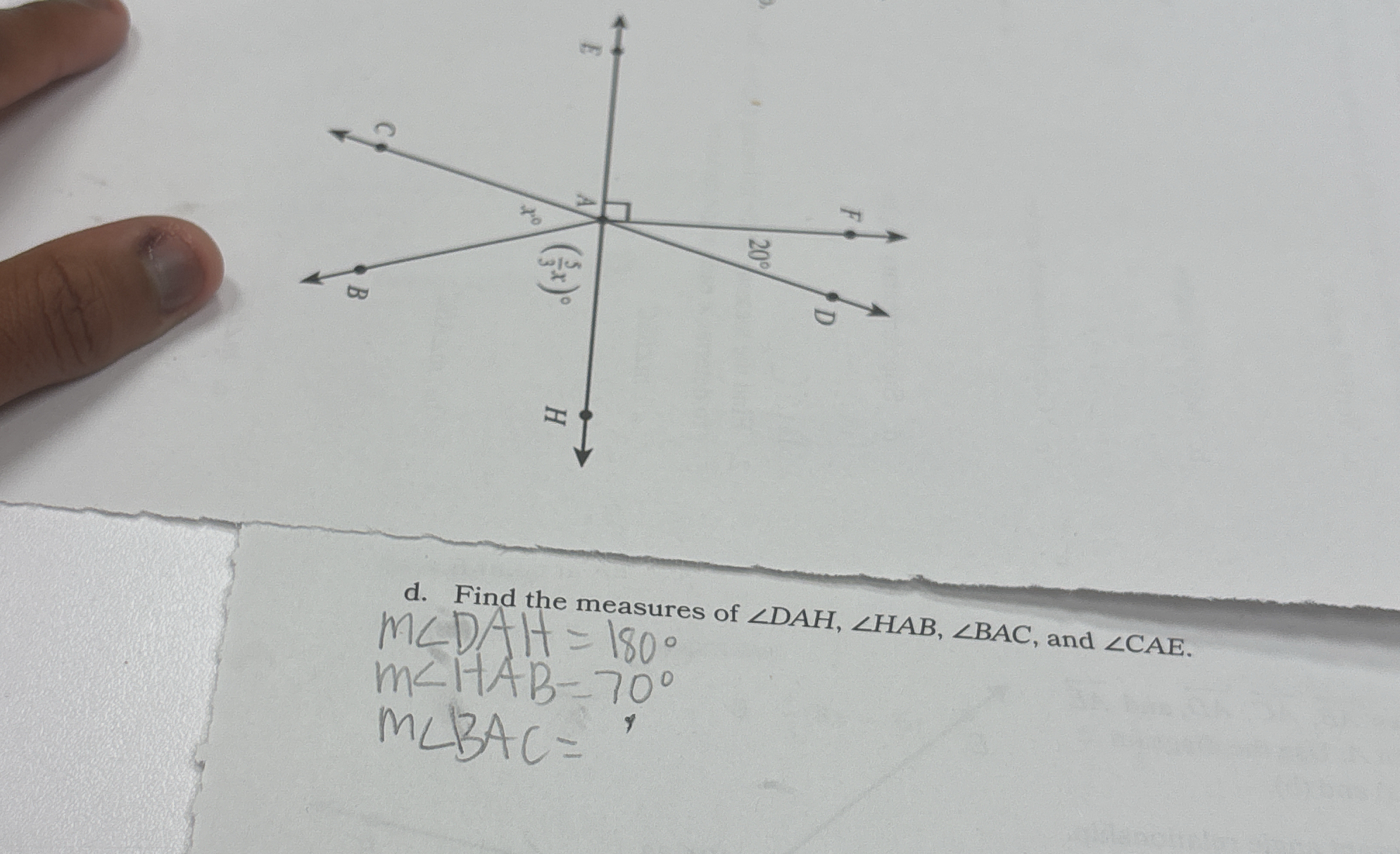
Find the measures of ∠DAH, ∠HAB, ∠BAC, and ∠CAE.
Understand the Problem
The question is asking to find the measures of specific angles given in a geometric diagram. It specifies angles ∠DAH, ∠HAB, ∠BAC, and ∠CAE, with some measures already indicated.
Answer
m∠DAH = $180^\circ$, m∠HAB = $70^\circ$, m∠BAC = $110^\circ$, m∠CAE = $110^\circ$.
Answer for screen readers
The measures are:
- m∠DAH = $180^\circ$
- m∠HAB = $70^\circ$
- m∠BAC = $110^\circ$
- m∠CAE = $110^\circ$
Steps to Solve
-
Identify Given Angles From the diagram:
- Measure of angle ∠DAH is given as $180^\circ$.
- Measure of angle ∠HAB is given as $70^\circ$.
-
Calculate Measure of ∠BAC Since angles ∠HAB and ∠BAC form a linear pair and lie on a straight line (line AB): $$ \text{m}∠BAC = 180^\circ - \text{m}∠HAB $$ Substituting the value: $$ \text{m}∠BAC = 180^\circ - 70^\circ = 110^\circ $$
-
Using Vertical Angles to Find ∠CAE Angles ∠BAC and ∠CAE are vertical angles, which means they are equal: $$ \text{m}∠CAE = \text{m}∠BAC $$ Therefore: $$ \text{m}∠CAE = 110^\circ $$
-
Summarize All Angles We have calculated:
- ∠DAH = $180^\circ$
- ∠HAB = $70^\circ$
- ∠BAC = $110^\circ$
- ∠CAE = $110^\circ$
The measures are:
- m∠DAH = $180^\circ$
- m∠HAB = $70^\circ$
- m∠BAC = $110^\circ$
- m∠CAE = $110^\circ$
More Information
These angles are calculated based on properties of straight lines and vertical angles. Knowing that linear pairs of angles sum to $180^\circ$ and vertical angles are always equal helps in solving the problem.
Tips
- Confusing adjacent angles with vertical angles. It's essential to identify their relationships correctly.
- Not remembering that a straight line forms a total angle of $180^\circ$. Ensure to always apply this principle when dealing with angles on a line.
AI-generated content may contain errors. Please verify critical information