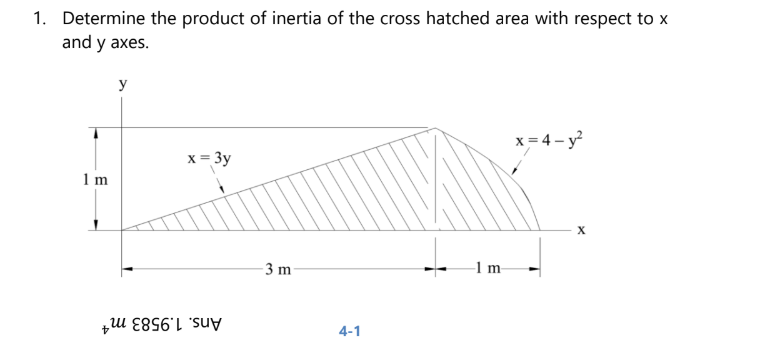
Determine the product of inertia of the cross hatched area with respect to x and y axes.

Steps to Solve

1. Identify the Shape and Boundary Equations

   The cross-hatched area is bounded by the equations (x = 3y) and (x = 4 - y^2). We will find the intersection points to determine the limits of integration.

2. Determine Intersection Points

   To find the intersection points, set the two equations equal to each other:

   $$3y = 4 - y^2$$

   Rearranging gives the equation:

   $$y^2 + 3y - 4 = 0$$

   Apply the quadratic formula (y = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}):

   Here, (a = 1), (b = 3), and (c = -4):

   $$y = \frac{-3 \pm \sqrt{3^2 - 4 \cdot 1 \cdot (-4)}}{2 \cdot 1}$$

   This will give us two values for (y):

   $$y = 1 \quad \text{and} \quad y = -4$$

   Since the area is bounded by (y) from (0) to (1), we will use these limits.

3. Set Up the Integral for Area (A)

   The area (A) of the cross-hatched region can be calculated as:

   $$A = \int_0^1 (4 - y^2 - 3y) , dy$$

   Simplifying the integral:

   $$A = \int_0^1 (1 - 3y + 4 - y^2) , dy$$

4. Integrate to Find the Area

   Evaluating the integral:

   $$A = \int_0^1 (1 - 3y + 4 - y^2) , dy = \left[y - \frac{3y^2}{2} + 4y - \frac{y^3}{3}\right]_0^1$$

   Calculate the definite integral and obtain the area (A).

5. Calculate the Centroid (x̄ and ȳ)

   The coordinates of the centroid can be found using:

   $$\bar{x} = \frac{1}{A} \int_0^1 x \cdot (4 - y^2 - 3y) , dy$$

   $$\bar{y} = \frac{1}{A} \int_0^1 y \cdot (4 - y^2 - 3y) , dy$$

   Use the calculated area to evaluate these integrals.

6. Determine the Product of Inertia (Ixy)

   The product of inertia can be calculated using the formula:

   $$I_{xy} = \int_A xy , dA$$

   Convert to appropriate limits and integrate across the defined area.

7. Final Calculation

   After evaluating all required integrals, substituting the centroid coordinates and computing the final values, we arrive at the values for the product of inertia with respect to the x and y axes.