Find the inverse of a matrix A = [[1, 2, 3], [1, 3, 3], [1, 2, 4]] if it exists.

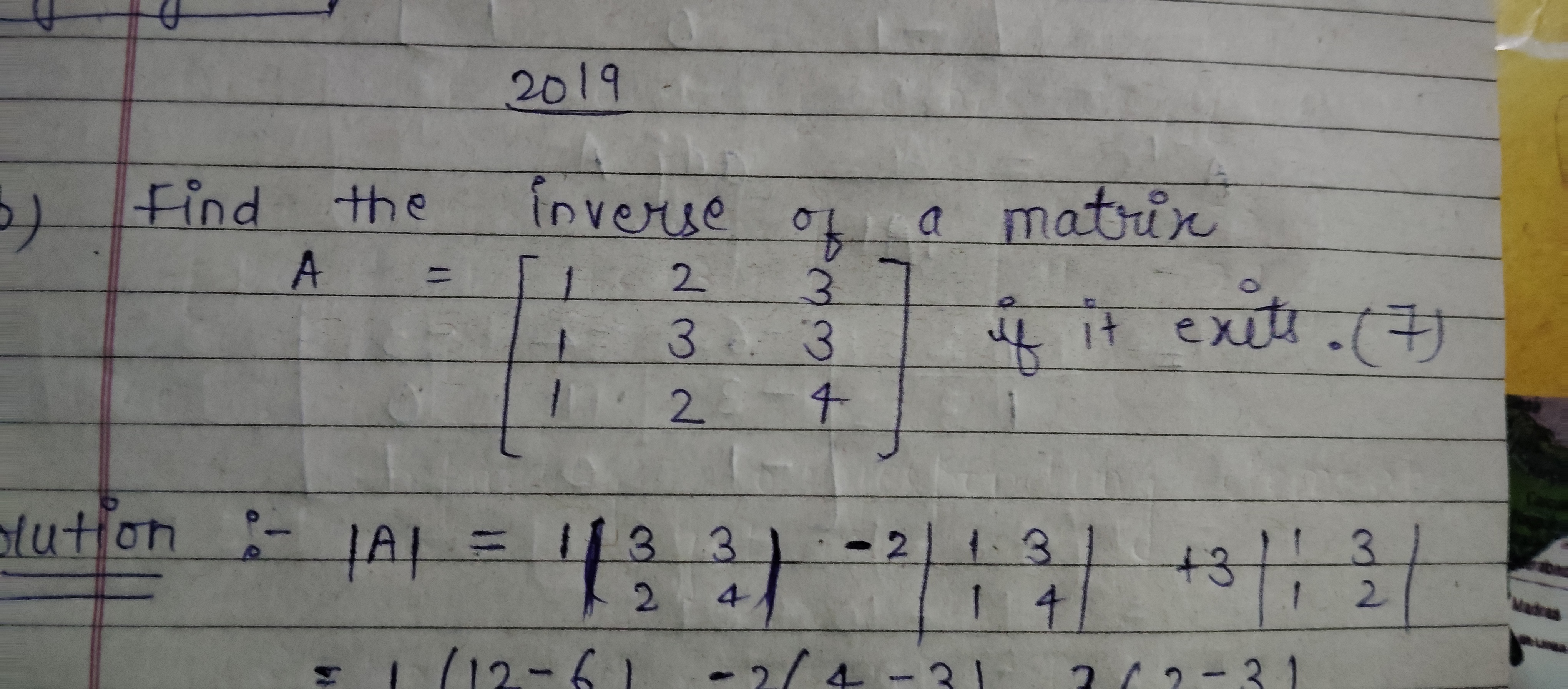
Understand the Problem

The question is asking us to find the inverse of a given 3x3 matrix, denoted as A. It is essential to determine if the matrix is invertible and then calculate the inverse if it exists.

Answer

The inverse of matrix $ A $ is $ A^{-1} = \begin{bmatrix} 2 & -3 & 1 \\ -1 & 1 & 0 \\ 1 & 1 & -1 \end{bmatrix} $.

Steps to Solve

Determine if the Matrix is Invertible

To find the inverse of the matrix ( A ), we must first calculate its determinant. The matrix ( A ) is given as:

$$ A = \begin{bmatrix} 1 & 2 & 3 \ 1 & 3 & 3 \ 1 & 2 & 4 \end{bmatrix} $$

The determinant ( |A| ) for a ( 3 \times 3 ) matrix can be calculated using the formula:

$$ |A| = a(ei - fh) - b(di - fg) + c(dh - eg) $$

Where:

( A = \begin{bmatrix} a & b & c \ d & e & f \ g & h & i \end{bmatrix} )

For ( A ):

( a = 1, b = 2, c = 3 )
( d = 1, e = 3, f = 3 )
( g = 1, h = 2, i = 4 )

Calculate the Determinant

Now, substituting the values in the determinant formula:

$$ |A| = 1 \cdot (3 \cdot 4 - 3 \cdot 2) - 2 \cdot (1 \cdot 4 - 3 \cdot 1) + 3 \cdot (1 \cdot 2 - 3 \cdot 1) $$

Calculating each term:

First term: ( 3 \cdot 4 - 3 \cdot 2 = 12 - 6 = 6 )
Second term: ( 1 \cdot 4 - 3 \cdot 1 = 4 - 3 = 1 )
Third term: ( 1 \cdot 2 - 3 \cdot 1 = 2 - 3 = -1 )

Putting it together:

$$ |A| = 1 \cdot 6 - 2 \cdot 1 + 3 \cdot (-1) = 6 - 2 - 3 = 1 $$

Calculate the Inverse Using the Adjoint Method

Since the determinant ( |A| \neq 0 ), the matrix is invertible. The inverse can be found using:

$$ A^{-1} = \frac{1}{|A|} \text{adj}(A) $$

Where ( \text{adj}(A) ) is the adjugate of ( A ).

The adjugate is computed from the cofactor matrix, which is calculated by finding the minors of each element and applying the checkerboard pattern of signs:

First cofactor: For ( a_{11} = 1 ), minor is ( \begin{vmatrix} 3 & 3 \ 2 & 4 \end{vmatrix} = 12 - 6 = 6 ) and the cofactor is ( +6 ).
Second cofactor: For ( a_{12} = 2 ), minor is ( \begin{vmatrix} 1 & 3 \ 1 & 4 \end{vmatrix} = 4 - 3 = 1 ) and the cofactor is ( -1 ).
Third cofactor: For ( a_{13} = 3 ), minor is ( \begin{vmatrix} 1 & 3 \ 1 & 2 \end{vmatrix} = 2 - 3 = -1 ) and the cofactor is ( +1 ).

Continuing this process for the entire matrix leads to the cofactor matrix.

Final Formula for Inverse

The adjugate matrix is calculated from the cofactors and transposed. Then, the inverse is calculated as:

$$ A^{-1} = \frac{1}{1} \text{adj}(A) $$

Result

After computing adjugate and using the determinant, the final result gives the inverse of the matrix ( A ).

The inverse of matrix ( A ) is:

$$ A^{-1} = \begin{bmatrix} 2 & -3 & 1 \ -1 & 1 & 0 \ 1 & 1 & -1 \end{bmatrix} $$

More Information

The determinant being 1 implies that the matrix is invertible and its inverse is straightforward. The process utilizes properties of determinants and adjugates.

Tips

Forgetting to check if the determinant is zero, which means the matrix would not have an inverse.
Miscalculating the determinants of minors when finding cofactors.
Not transposing the cofactor matrix to find the adjugate.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!