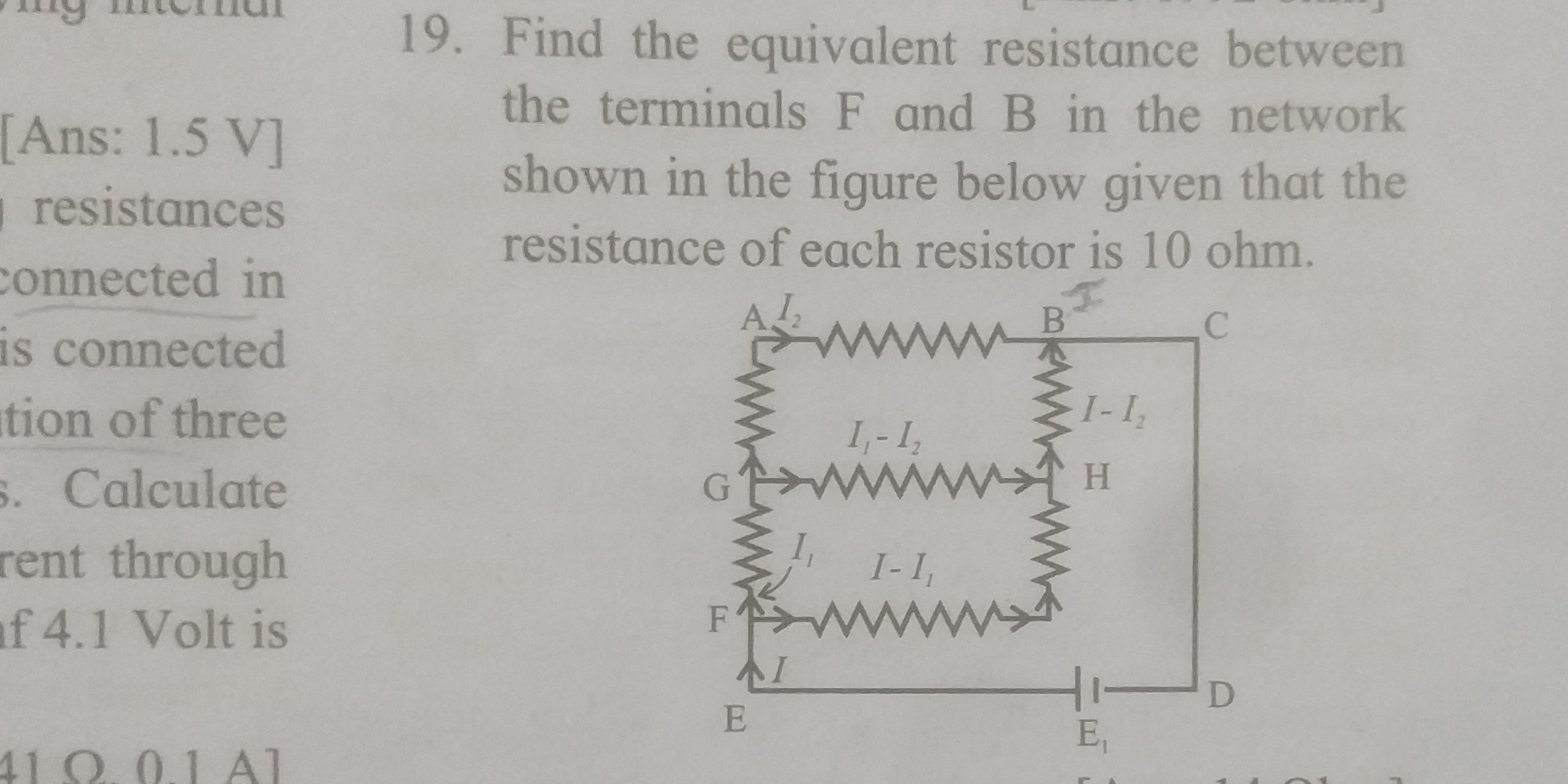
Find the equivalent resistance between the terminals F and B in the network shown in the figure below given that the resistance of each resistor is 10 ohm.
Understand the Problem
The question is asking to find the equivalent resistance between terminals F and B in a given circuit diagram where each resistor has a resistance of 10 ohms.
Answer
The equivalent resistance $R_{eq}$ between terminals F and B is $6 \, \text{ohms}$.
Answer for screen readers
The equivalent resistance $R_{eq}$ between terminals F and B is $6 , \text{ohms}$.
Steps to Solve
- Identify the Arrangement of Resistors
From the diagram, it appears that resistors are arranged in a combination of series and parallel. Resistances need to be grouped accordingly.
- Calculate Equivalent Resistance of Parallel and Series Combinations
For resistors in parallel, use the formula: $$ \frac{1}{R_{eq}} = \frac{1}{R_1} + \frac{1}{R_2} + ... $$
For resistors in series, use: $$ R_{eq} = R_1 + R_2 + ... $$
- Group Resistors from F to B
From F to B, we first deal with resistors GH and AE: For resistors in parallel, since they're all 10 ohms, $$ \frac{1}{R_{GH}} = \frac{1}{10} + \frac{1}{10} = \frac{2}{10} $$ Thus, $$ R_{GH} = \frac{10}{2} = 5 , \text{ohms} $$
Next, consider resistor FB (10 ohms) in series with $R_{GH}$: $$ R_{FB-GH} = R_{GH} + R_{FB} = 5 + 10 = 15 , \text{ohms} $$
- Consider Total Resistance from F to B
Continuing the equivalent resistance calculation:
- Now, resistors DC (10 ohms) and AB (10 ohms) are still in parallel with the previous combination: Using the parallel formula again: $$ \frac{1}{R_{total}} = \frac{1}{15} + \frac{1}{10} $$ Finding a common denominator (30): $$ \frac{1}{R_{total}} = \frac{2}{30} + \frac{3}{30} = \frac{5}{30} $$
Thus, $$ R_{total} = \frac{30}{5} = 6 , \text{ohms} $$
- Final Equivalent Resistance between F and B
Thus, the equivalent resistance between terminals F and B is: $$ R_{eq} = 6 , \text{ohms} $$
The equivalent resistance $R_{eq}$ between terminals F and B is $6 , \text{ohms}$.
More Information
This example illustrates how to systematically approach circuits with a mix of parallel and series resistors. Understanding how to convert these configurations into their equivalent resistances is a crucial skill in circuit analysis.
Tips
- Misidentifying series and parallel configurations: Always double-check how resistors are connected in the circuit.
- Failing to simplify systematically: It’s important to break down complex circuits step-by-step.
AI-generated content may contain errors. Please verify critical information