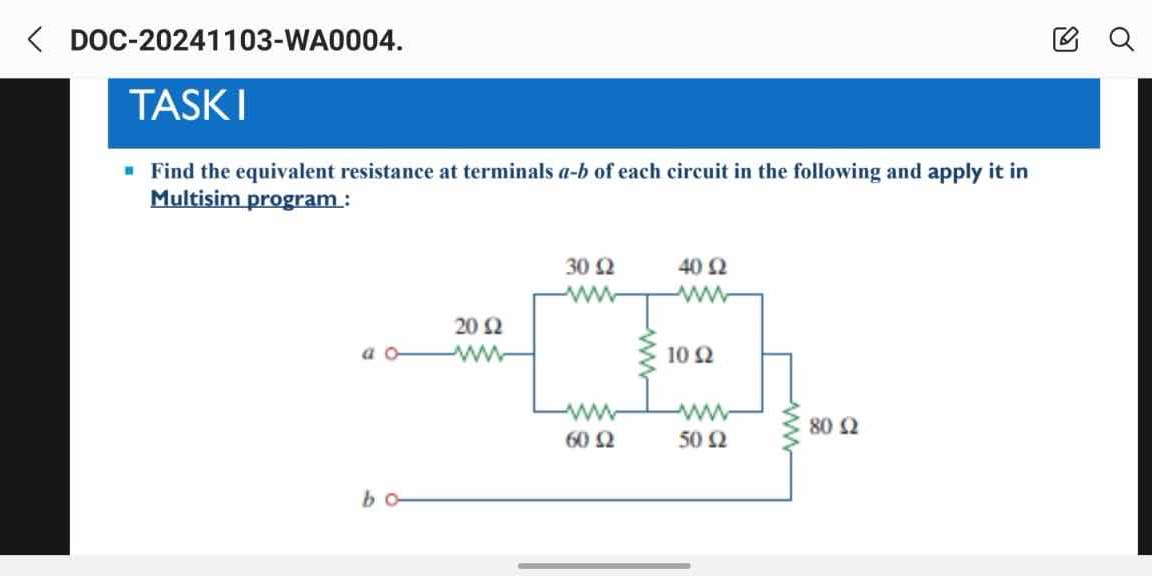
Find the equivalent resistance at terminals a-b of each circuit in the following and apply it in Multisim program.

Steps to Solve

1. Identify Series and Parallel Resistors

   Start by analyzing the circuit to group resistors in series and parallel. In this circuit:

   • The resistors 10 Ω, 50 Ω, and 80 Ω are in parallel.
   • The 30 Ω and 40 Ω resistors are in series.

2. Calculate Equivalent Resistance for Parallel Resistors

   For the parallel resistors (10 Ω, 50 Ω, 80 Ω), use the formula for equivalent resistance in parallel:

   $$ \frac{1}{R_{eq}} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} $$

   Here, ( R_1 = 10 , \Omega ), ( R_2 = 50 , \Omega ), and ( R_3 = 80 , \Omega ).

3. Combine the Resistances

   Calculate ( R_{eq} ) for the parallel section:

   $$ \frac{1}{R_{eq}} = \frac{1}{10} + \frac{1}{50} + \frac{1}{80} $$

   Simplifying gives:

   $$ \frac{1}{R_{eq}} = 0.1 + 0.02 + 0.0125 = 0.1325 $$

   Therefore,

   $$ R_{eq} = \frac{1}{0.1325} \approx 7.53 , \Omega $$

4. Combine with Series Resistors

   Now, include the previously identified series resistors (30 Ω and 40 Ω):

   $$ R_{total} = R_{eq} + 30 + 40 $$

   Substitute ( R_{eq} ) to find:

   $$ R_{total} = 7.53 + 30 + 40 = 77.53 , \Omega $$