Find the equation of the line XY. Show that Z lies on the straight line that passes through X & Y.
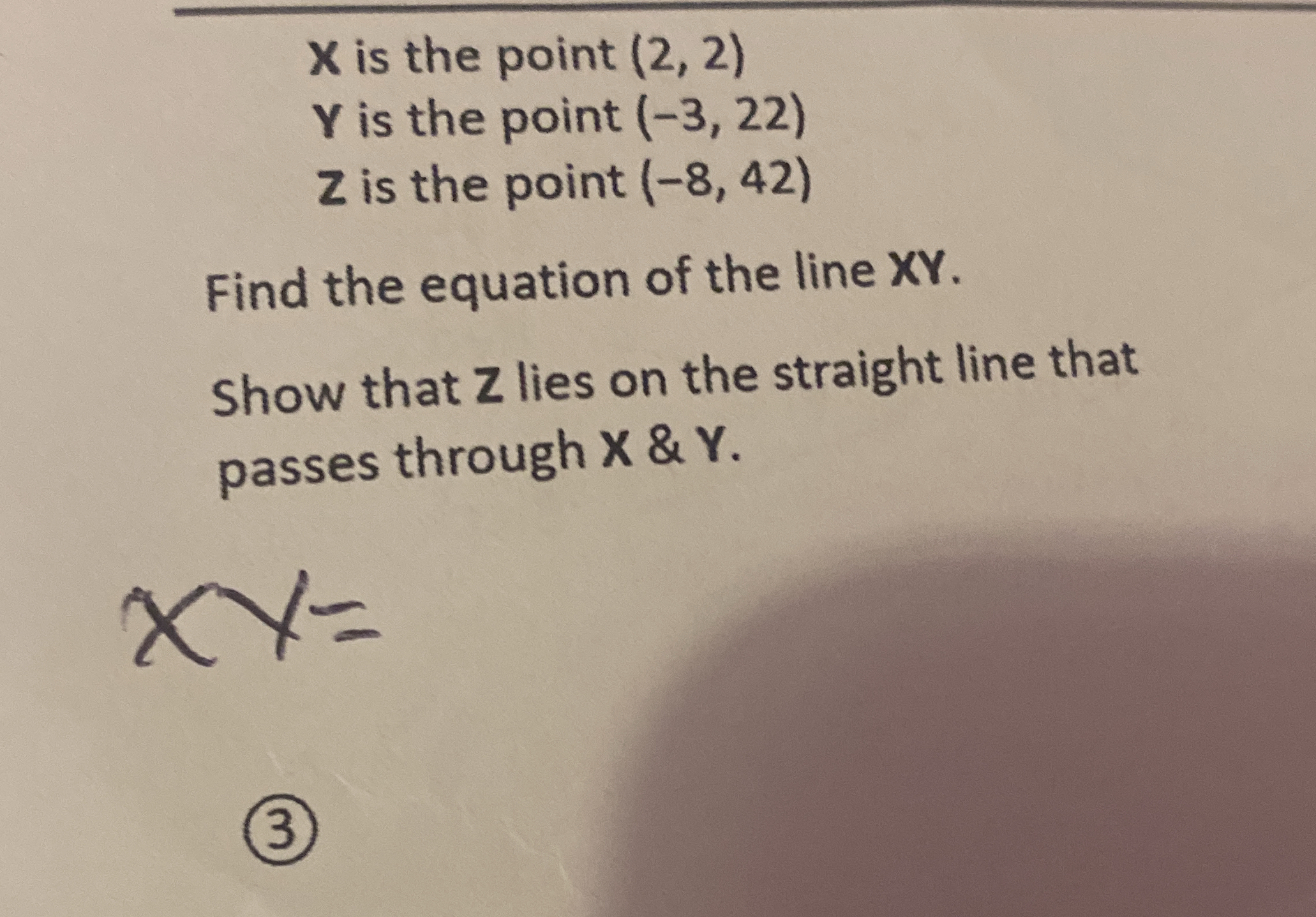
Understand the Problem
The question is asking to find the equation of the line that passes through two given points (X and Y) and to verify whether a third point (Z) lies on this line. This involves using the coordinates of the points to derive the line's equation and then testing the coordinates of Z against this equation.
Answer
The equation of the line is $y = -4x + 10$. Point Z lies on this line.
Answer for screen readers
The equation of the line ( XY ) is
$$ y = -4x + 10 $$
and point Z lies on the line.
Steps to Solve
- Identify the coordinates of points X and Y
Point ( X ) has coordinates ( (2, 2) ) and point ( Y ) has coordinates ( (-3, 22) ).
- Calculate the slope (m) of the line passing through points X and Y
The formula for the slope ( m ) between two points ( (x_1, y_1) ) and ( (x_2, y_2) ) is given by:
$$ m = \frac{y_2 - y_1}{x_2 - x_1} $$
Applying the coordinates:
- ( (x_1, y_1) = (2, 2) )
- ( (x_2, y_2) = (-3, 22) )
Substituting values:
$$ m = \frac{22 - 2}{-3 - 2} = \frac{20}{-5} = -4 $$
- Use point-slope form to find the line's equation
The point-slope form of a line is:
$$ y - y_1 = m(x - x_1) $$
Using point ( X (2, 2) ):
$$ y - 2 = -4(x - 2) $$
- Rearranging to slope-intercept form
Expanding and rearranging the equation:
$$ y - 2 = -4x + 8 $$
Adding 2 to both sides:
$$ y = -4x + 10 $$
- Verify if point Z lies on the line
Point ( Z ) has coordinates ( (-8, 42) ). Substitute ( x = -8 ) into the line equation:
$$ y = -4(-8) + 10 $$
Calculating:
$$ y = 32 + 10 = 42 $$
Since the calculated ( y ) value matches the ( y ) coordinate of point Z, point Z lies on the line.
The equation of the line ( XY ) is
$$ y = -4x + 10 $$
and point Z lies on the line.
More Information
The slope of the line indicates that for every unit increase in ( x ), ( y ) decreases by 4 units. The equation is now in slope-intercept form, which easily allows you to identify the slope and y-intercept.
Tips
- Incorrect slope calculation: Make sure to subtract the y-coordinates in the correct order, which affects the sign of the slope.
- Misapplication of point-slope form: Ensure that you substitute ( m ), ( x_1 ), and ( y_1 ) correctly based on the chosen point.
- Not verifying the point Z: Always substitute back to confirm that the point lies on the line after you've derived the equation.
AI-generated content may contain errors. Please verify critical information