Find the direction vector of vector PQ, where P is (-9, 3) and Q is (-4, 8).
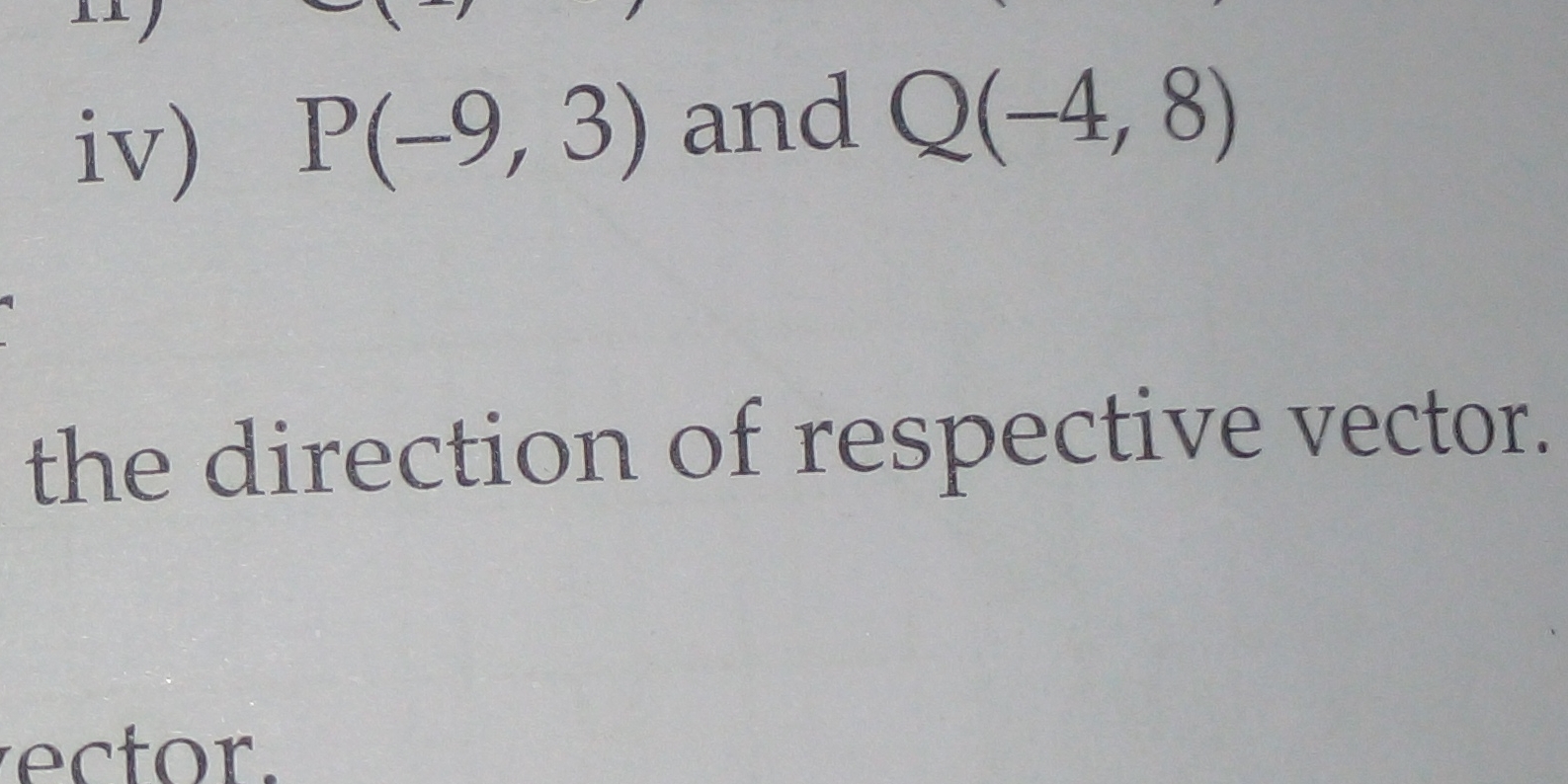
Understand the Problem
The question involves finding the direction vector given two points P and Q. To find the direction vector, you subtract the coordinates of the initial point P from the terminal point Q.
Answer
$\langle 5, 5 \rangle$
Answer for screen readers
$\vec{v} = \langle 5, 5 \rangle$
Steps to Solve
- Identify the coordinates of points P and Q
The coordinates are given as P(-9, 3) and Q(-4, 8).
- Calculate the difference in x-coordinates
Subtract the x-coordinate of P from the x-coordinate of Q: $Q_x - P_x = -4 - (-9) = -4 + 9 = 5$
- Calculate the difference in y-coordinates
Subtract the y-coordinate of P from the y-coordinate of Q: $Q_y - P_y = 8 - 3 = 5$
- Form the direction vector
The direction vector is formed by the differences calculated in the previous steps: $\vec{v} = \langle 5, 5 \rangle$
$\vec{v} = \langle 5, 5 \rangle$
More Information
The direction vector $\langle 5, 5 \rangle$ represents the displacement from point P to point Q. It indicates a movement of 5 units in the positive x-direction and 5 units in the positive y-direction.
Tips
A common mistake is subtracting the coordinates in the wrong order (i.e., P - Q instead of Q - P), which would result in a vector pointing in the opposite direction. Also, sign errors while subtracting negative numbers are common.
AI-generated content may contain errors. Please verify critical information