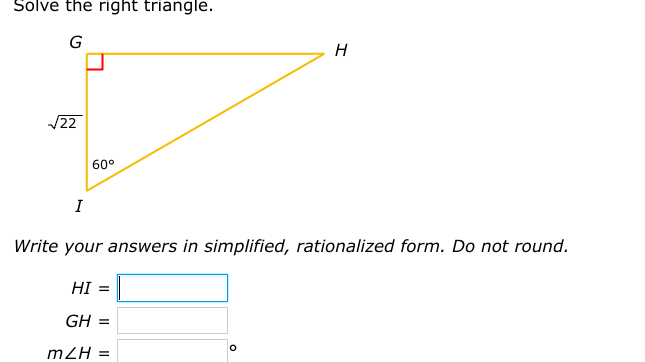
Solve the right triangle. Given side GI = √22 and angle I = 60°, find sides HI, GH, and the measure of angle H. Write your answers in simplified, rationalized form. Do not round. Solve the right triangle. Given side GI = √22 and angle I = 60°, find sides HI, GH, and the measure of angle H. Write your answers in simplified, rationalized form. Do not round. Read more

Steps to Solve

1. Identify Given Information

We are given that side $GI = \sqrt{22}$ and angle $H = 60^\circ$. We need to find sides $HI$ and $GH$ and the measure of angle $H$.

2. Determine Angle G

Since it is a right triangle, we know that the angles in a triangle add up to $180^\circ$. The triangle's right angle at G means:

$$ m\angle G = 90^\circ $$

Now, we can find angle $I$ using:

$$ m\angle I = 180^\circ - m\angle G - m\angle H = 180^\circ - 90^\circ - 60^\circ = 30^\circ $$

3. Use Trigonometric Ratios to Find HI

We can use the sine function to find side $HI$:

$$ \sin(60^\circ) = \frac{HI}{GI} $$

Substituting the known values:

$$ \sin(60^\circ) = \frac{HI}{\sqrt{22}} $$

Since $\sin(60^\circ) = \frac{\sqrt{3}}{2}$, we have:

$$ \frac{\sqrt{3}}{2} = \frac{HI}{\sqrt{22}} $$

Now solve for $HI$:

$$ HI = \sqrt{22} \cdot \frac{\sqrt{3}}{2} = \frac{\sqrt{66}}{2} $$

4. Use Trigonometric Ratios to Find GH

For side $GH$, we can use the cosine function:

$$ \cos(60^\circ) = \frac{GH}{GI} $$

Substituting known values gives:

$$ \cos(60^\circ) = \frac{GH}{\sqrt{22}} $$

Since $\cos(60^\circ) = \frac{1}{2}$, we get:

$$ \frac{1}{2} = \frac{GH}{\sqrt{22}} $$

Now we can solve for $GH$:

$$ GH = \sqrt{22} \cdot \frac{1}{2} = \frac{\sqrt{22}}{2} $$

5. Final Measures of Angles

Angle $H$ is already given as $60^\circ$.