Find the critical points of f(x) = x^3 - 12x - 5 and identify the open intervals on which f is increasing and on which f is decreasing.
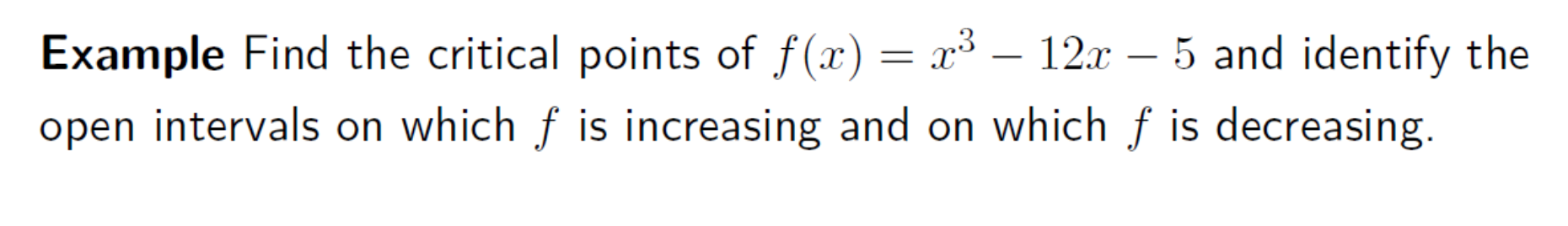
Understand the Problem
The question is asking to find the critical points of the function f(x) = x^3 - 12x - 5 and to determine the open intervals where the function is increasing and decreasing. This involves taking the derivative, finding the critical points, and analyzing the sign of the derivative.
Answer
Critical points: \( x = -2, 2 \); Increasing: \( (-\infty, -2) \) and \( (2, \infty) \); Decreasing: \( (-2, 2) \).
Answer for screen readers
The critical points of the function ( f(x) = x^3 - 12x - 5 ) are ( x = -2 ) and ( x = 2 ). The function is increasing on the intervals ( (-\infty, -2) ) and ( (2, \infty) ), and decreasing on the interval ( (-2, 2) ).
Steps to Solve
- Find the derivative of the function
To find the critical points, we first need to calculate the derivative of the function ( f(x) = x^3 - 12x - 5 ).
The derivative is:
$$ f'(x) = 3x^2 - 12 $$
- Set the derivative to zero
Next, we set the derivative equal to zero to find the critical points:
$$ 3x^2 - 12 = 0 $$
- Solve for critical points
Now we solve for ( x ):
$$ 3x^2 = 12 $$
Dividing both sides by 3 gives:
$$ x^2 = 4 $$
Taking the square root:
$$ x = 2 \quad \text{or} \quad x = -2 $$
So, the critical points are ( x = -2 ) and ( x = 2 ).
- Test intervals for increasing or decreasing behavior
Next, we will test the intervals around the critical points to determine where the function is increasing or decreasing. The intervals to test are ( (-\infty, -2) ), ( (-2, 2) ), and ( (2, \infty) ).
-
Choose a test point in each interval and evaluate ( f'(x) ):
- For ( x = -3 ) in ( (-\infty, -2) ):
$$ f'(-3) = 3(-3)^2 - 12 = 27 - 12 = 15 \quad (\text{positive, increasing}) $$
- For ( x = 0 ) in ( (-2, 2) ):
$$ f'(0) = 3(0)^2 - 12 = -12 \quad (\text{negative, decreasing}) $$
- For ( x = 3 ) in ( (2, \infty) ):
$$ f'(3) = 3(3)^2 - 12 = 27 - 12 = 15 \quad (\text{positive, increasing}) $$
- Summarize the intervals of increase and decrease
From the tests:
-
The function is increasing on ( (-\infty, -2) ) and ( (2, \infty) ).
-
The function is decreasing on ( (-2, 2) ).
The critical points of the function ( f(x) = x^3 - 12x - 5 ) are ( x = -2 ) and ( x = 2 ). The function is increasing on the intervals ( (-\infty, -2) ) and ( (2, \infty) ), and decreasing on the interval ( (-2, 2) ).
More Information
Understanding critical points and their corresponding intervals is essential in calculus. It helps identify where a function changes from increasing to decreasing or vice versa, which is important for graphing the function and optimizing real-world scenarios.
Tips
- Forgetting to check the sign of the derivative in each interval.
- Confusing increasing and decreasing intervals. Remember: if ( f'(x) > 0 ), the function is increasing; if ( f'(x) < 0 ), the function is decreasing.
