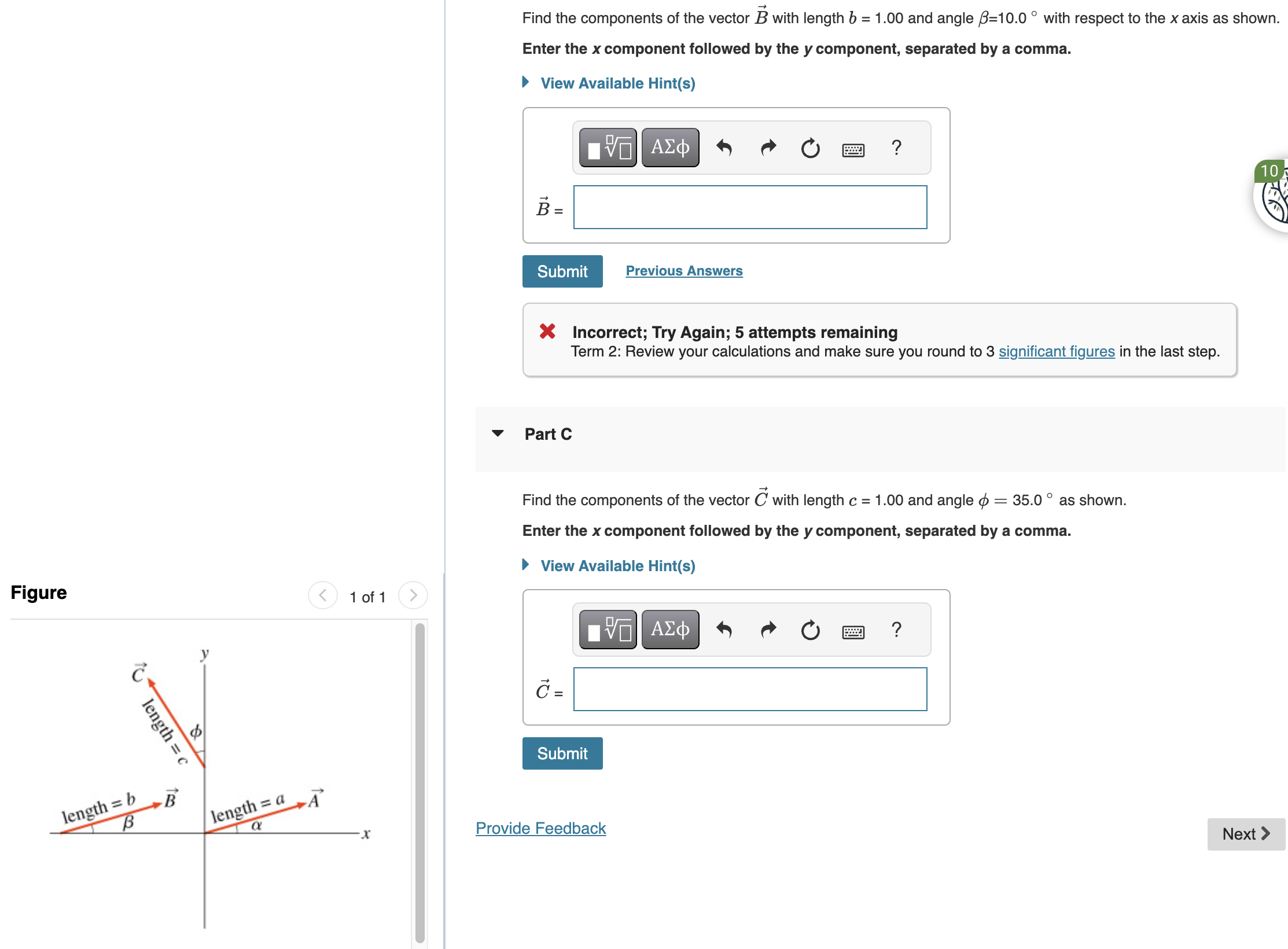
Find the components of the vector \vec{B} with length b = 1.00 and angle \beta = 10.0° with respect to the x-axis. Enter the x component followed by the y component, separated by a... Find the components of the vector \vec{B} with length b = 1.00 and angle \beta = 10.0° with respect to the x-axis. Enter the x component followed by the y component, separated by a comma. Find the components of the vector \vec{C} with length c = 1.00 and angle \phi = 35.0° as shown. Enter the x component followed by the y component, separated by a comma.
Understand the Problem
The question involves calculating the components of vectors based on their lengths and angles with respect to the x-axis. We need to apply trigonometric functions to find the x and y components for the specified vectors.
Answer
For vector \( \vec{B} \): \( 0.985, 0.174 \); for vector \( \vec{C} \): \( 0.819, 0.574 \).
Answer for screen readers
For vector ( \vec{B} ): ( B_x \approx 0.985, B_y \approx 0.174 )
For vector ( \vec{C} ): ( C_x \approx 0.819, C_y \approx 0.574 )
Steps to Solve
-
Identify the vector's components For the vector ( \vec{B} ) with length ( b = 1.00 , \text{units} ) and angle ( \beta = 10.0^\circ ):
- The x-component is given by: $$ B_x = b \cdot \cos(\beta) $$
- The y-component is given by: $$ B_y = b \cdot \sin(\beta) $$
-
Calculate the x-component of vector B Substituting the given values: $$ B_x = 1.00 \cdot \cos(10.0^\circ) $$
-
Calculate the y-component of vector B Substituting the given values: $$ B_y = 1.00 \cdot \sin(10.0^\circ) $$
-
Perform the calculations for vector B Using a calculator:
- ( \cos(10.0^\circ) \approx 0.9848 )
- ( \sin(10.0^\circ) \approx 0.1736 )
So: $$ B_x \approx 1.00 \cdot 0.9848 \approx 0.985 $$ $$ B_y \approx 1.00 \cdot 0.1736 \approx 0.174 $$
-
Combine the components for vector B The components for vector ( \vec{B} ) are: $$ B_x, B_y \approx 0.985, 0.174 $$
-
Do the same for vector C For vector ( \vec{C} ) with length ( c = 1.00 , \text{units} ) and angle ( \phi = 35.0^\circ ):
- The x-component is: $$ C_x = c \cdot \cos(\phi) $$
- The y-component is: $$ C_y = c \cdot \sin(\phi) $$
-
Calculate the x-component of vector C Substituting the given values: $$ C_x = 1.00 \cdot \cos(35.0^\circ) $$
-
Calculate the y-component of vector C Substituting the given values: $$ C_y = 1.00 \cdot \sin(35.0^\circ) $$
-
Perform the calculations for vector C Using a calculator:
- ( \cos(35.0^\circ) \approx 0.8192 )
- ( \sin(35.0^\circ) \approx 0.5736 )
So: $$ C_x \approx 1.00 \cdot 0.8192 \approx 0.819 $$ $$ C_y \approx 1.00 \cdot 0.5736 \approx 0.574 $$
-
Combine the components for vector C The components for vector ( \vec{C} ) are: $$ C_x, C_y \approx 0.819, 0.574 $$
For vector ( \vec{B} ): ( B_x \approx 0.985, B_y \approx 0.174 )
For vector ( \vec{C} ): ( C_x \approx 0.819, C_y \approx 0.574 )
More Information
The components of a vector represent its projections on the x-axis and y-axis. These projections are crucial in physics for understanding forces, velocities, and other vector quantities.
Tips
- Forgetting to use degrees when calculating trigonometric functions.
- Miscalculating (\cos) and (\sin) values, leading to incorrect components.
- Not rounding to the required number of significant figures.
AI-generated content may contain errors. Please verify critical information