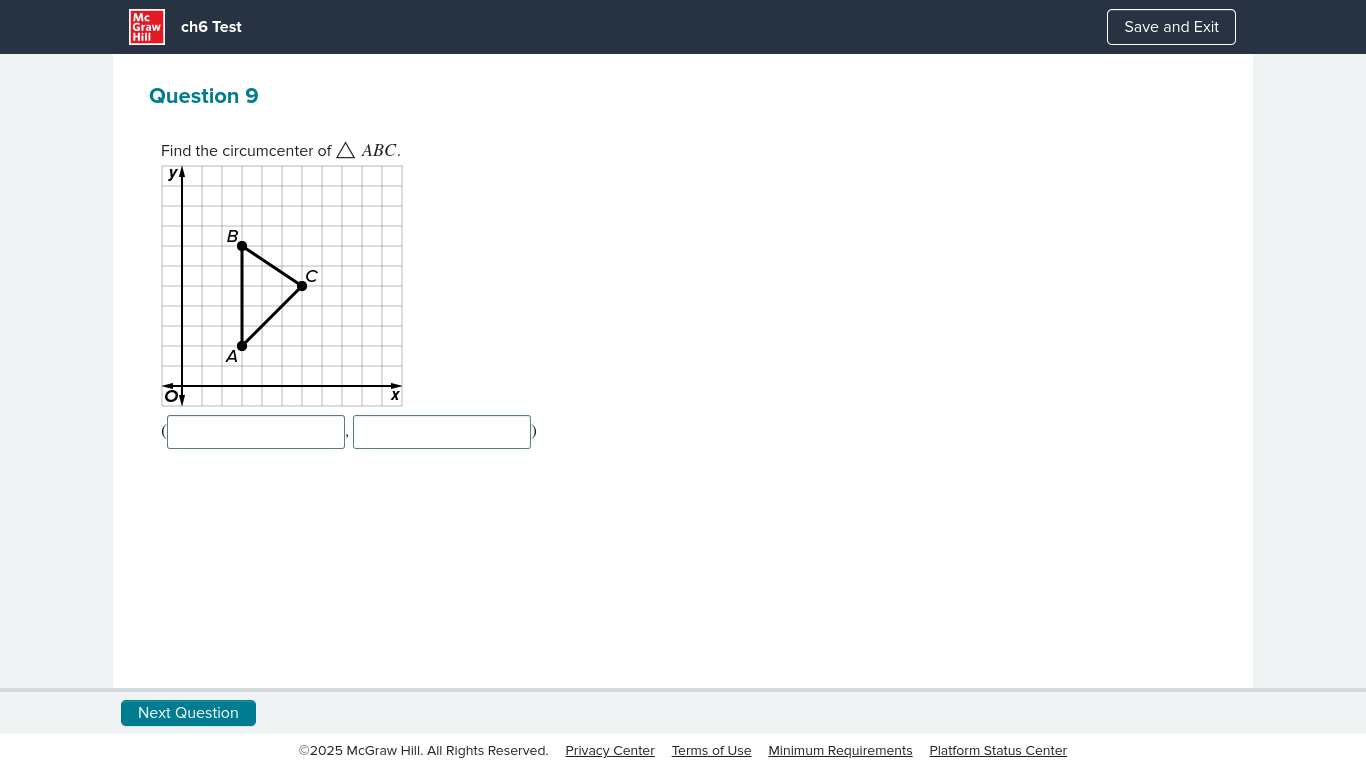
Find the circumcenter of triangle ABC.

Steps to Solve

1. Identify the coordinates of the points A, B, and C From the graph, find the coordinates of the vertices of triangle ABC.

   • ( A(0, 0) )
   • ( B(2, 5) )
   • ( C(6, 2) )

2. Find the midpoints of segments AB and AC The midpoint formula is given by:

   $$ M(x, y) = \left( \frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2} \right) $$

   Calculate the midpoints:

   • Midpoint of ( AB ): $$ M_{AB} = \left( \frac{0 + 2}{2}, \frac{0 + 5}{2} \right) = (1, 2.5) $$
   • Midpoint of ( AC ): $$ M_{AC} = \left( \frac{0 + 6}{2}, \frac{0 + 2}{2} \right) = (3, 1) $$

3. Determine the slopes of segments AB and AC The slope formula is:

   $$ m = \frac{y_2 - y_1}{x_2 - x_1} $$

   Calculate the slopes:

   • Slope of ( AB ): $$ m_{AB} = \frac{5 - 0}{2 - 0} = \frac{5}{2} $$
   • Slope of ( AC ): $$ m_{AC} = \frac{2 - 0}{6 - 0} = \frac{1}{3} $$

4. Find the slopes of the perpendicular bisectors The slope of a line perpendicular to another is the negative reciprocal:

   $$ m_{perpendicular} = -\frac{1}{m} $$

   Calculate the slopes:

   • Slope of the perpendicular bisector of ( AB ): $$ m_{perpendicular AB} = -\frac{2}{5} $$
   • Slope of the perpendicular bisector of ( AC ): $$ m_{perpendicular AC} = -3 $$

5. Write the equations of the perpendicular bisectors Use the point-slope form of a line:

   $$ y - y_1 = m(x - x_1) $$

   • Equation of perpendicular bisector of ( AB ): $$ y - 2.5 = -\frac{2}{5}(x - 1) $$
   • Equation of perpendicular bisector of ( AC ): $$ y - 1 = -3(x - 3) $$

6. Solve the equations to find the circumcenter Substitute and simplify both equations to find the intersection point.

   Solving:

   • From ( y - 2.5 = -\frac{2}{5}(x - 1) ): $$ y = -\frac{2}{5}x + \frac{2}{5} + 2.5 = -\frac{2}{5}x + 2.7 $$

   • From ( y - 1 = -3(x - 3) ): $$ y = -3x + 10 $$

   Set the equations equal to find the ( x ): $$ -\frac{2}{5}x + 2.7 = -3x + 10 $$

   Solving this will give the required coordinates of the circumcenter.