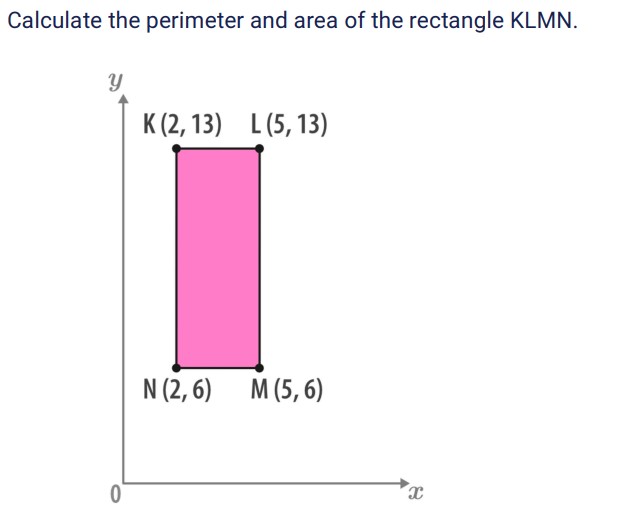
Calculate the perimeter and area of the rectangle KLNM.
Understand the Problem
The question is asking to find the perimeter and area of the rectangle KLNM using the coordinates provided for each vertex. The approach involves calculating the lengths of the sides of the rectangle first, then applying the formulas for perimeter and area.
Answer
The perimeter is $20$ and the area is $21$.
Answer for screen readers
The perimeter of the rectangle KLNM is $20$ and the area is $21$.
Steps to Solve
- Identify the coordinates of the vertices The coordinates of the rectangle KLNM are given as:
- K (2, 13)
- L (5, 13)
- N (2, 6)
- M (5, 6)
- Calculate the length of the sides The length of the rectangle can be calculated using the distance between points K and L (horizontal side) and N and M (vertical side).
- Length (horizontal) = (x_L - x_K = 5 - 2 = 3)
- Width (vertical) = (y_K - y_N = 13 - 6 = 7)
- Calculate the perimeter The perimeter (P) of a rectangle is given by the formula: $$ P = 2 \times (length + width) $$
Substituting the values we found: $$ P = 2 \times (3 + 7) = 2 \times 10 = 20 $$
- Calculate the area The area (A) of a rectangle is given by the formula: $$ A = length \times width $$
Substituting the values: $$ A = 3 \times 7 = 21 $$
The perimeter of the rectangle KLNM is $20$ and the area is $21$.
More Information
Rectangles have opposite sides that are equal in length. The perimeter gives the total distance around the rectangle, while the area measures the space contained within it. This problem illustrates how coordinates can be used to derive geometric properties.
Tips
- Mixing up length and width when doing calculations. Always label and check the sides carefully.
- Incorrectly applying the formulas for perimeter and area. Ensure that the correct formulas are used for rectangles.
AI-generated content may contain errors. Please verify critical information