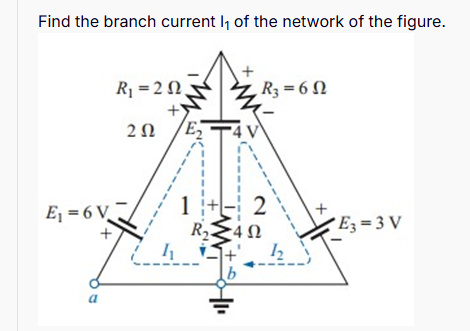
Find the branch current I1 of the network of the figure.
Understand the Problem
The question is asking to determine the branch current I1 in the given electrical network, which involves analyzing the circuit with resistances and voltage sources provided in the figure.
Answer
$I_1 = 1 \, A$
Answer for screen readers
The branch current $I_1$ is $1 , A$.
Steps to Solve
- Identify Nodes and Branch Currents
Label the nodes and currents in the circuit. Let current $I_1$ flow from node $a$ to node $b$, and $I_2$ be the current that returns through the $R_2$ resistor.
- Apply Kirchhoff's Current Law (KCL)
At node $b$, the algebraic sum of currents must equal zero:
$$ I_1 - I_2 = 0 $$
This gives us:
$$ I_1 = I_2 $$
- Apply Kirchhoff's Voltage Law (KVL)
For the loop containing $E_1$, $R_1$, and $R_2$, apply KVL:
$$ -E_1 + I_1 \cdot R_1 + I_2 \cdot R_2 = 0 $$
Substituting the values:
$$ -6 + I_1 \cdot 2 + I_2 \cdot 4 = 0 $$
- Express $I_2$ in terms of $I_1$
Since $I_2 = I_1,$ substitute in the KVL equation:
$$ -6 + I_1 \cdot 2 + I_1 \cdot 4 = 0 $$
Combine like terms:
$$ -6 + 6 I_1 = 0 $$
- Solve for $I_1$
Rearranging gives:
$$ 6 I_1 = 6 $$
Dividing both sides by 6 yields:
$$ I_1 = 1 , A $$
The branch current $I_1$ is $1 , A$.
More Information
In this circuit, we applied Kirchhoff's laws to find the current in a simple triangular circuit structure. Knowing how to manipulate these equations is essential in circuit analysis.
Tips
- Confusing the direction of current flow can lead to incorrect equations.
- Not applying KCL or KVL correctly can result in missing solutions.
- Neglecting to substitute the relationship between $I_1$ and $I_2$ might complicate the math unnecessarily.
AI-generated content may contain errors. Please verify critical information