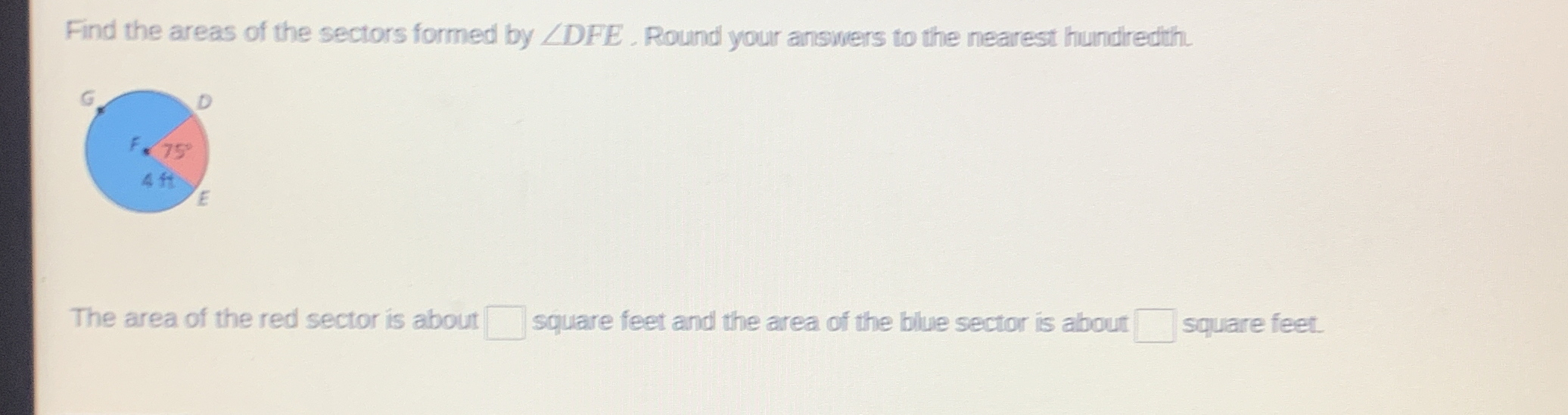
Find the areas of the sectors formed by angle DFE. Round your answers to the nearest hundredth. The area of the red sector is about __ square feet and the area of the blue sector i... Find the areas of the sectors formed by angle DFE. Round your answers to the nearest hundredth. The area of the red sector is about __ square feet and the area of the blue sector is about __ square feet.
Understand the Problem
The question is asking to find the areas of two sectors of a circle based on a given angle and radius. It requires the application of the formula for the area of a sector, which is A = (θ/360) * πr², where θ is the angle in degrees and r is the radius. The areas must be rounded to the nearest hundredth.
Answer
Red sector area: $10.55$ square feet, Blue sector area: $39.45$ square feet.
Answer for screen readers
The area of the red sector is about $10.55$ square feet and the area of the blue sector is about $39.45$ square feet.
Steps to Solve
-
Identify given values The problem states that the radius $r$ of the circle is 4 ft and the angle $\theta$ for the red sector is 75 degrees.
-
Calculate area of the red sector Use the formula for the area of a sector: $$ A = \frac{\theta}{360} \times \pi r^2 $$
Substituting the values: $$ A_{red} = \frac{75}{360} \times \pi \times (4)^2 $$
-
Evaluate the area of the red sector Calculate the area: $$ A_{red} = \frac{75}{360} \times \pi \times 16 $$ $$ A_{red} \approx \frac{75}{360} \times 50.27 \approx 10.55 $$ (rounded to two decimal places)
-
Calculate the area of the blue sector Since the blue sector corresponds to the remaining part of the circle, its angle is: $$ \theta_{blue} = 360 - 75 = 285 \text{ degrees} $$
Use the same formula: $$ A_{blue} = \frac{285}{360} \times \pi \times (4)^2 $$
- Evaluate the area of the blue sector Calculate the area: $$ A_{blue} = \frac{285}{360} \times \pi \times 16 $$ $$ A_{blue} \approx \frac{285}{360} \times 50.27 \approx 39.45 $$ (rounded to two decimal places)
The area of the red sector is about $10.55$ square feet and the area of the blue sector is about $39.45$ square feet.
More Information
The area of a sector reflects the portion of the circle that corresponds to a given angle. In this problem, we've found that the red sector (75 degrees) occupies a smaller area than the blue sector (285 degrees), demonstrating how the angle influences sector size.
Tips
- Forgetting to round the final answers to the nearest hundredth.
- Not realizing that the remainder of the circle's degrees (360 - angle) should be used for the second sector.
AI-generated content may contain errors. Please verify critical information