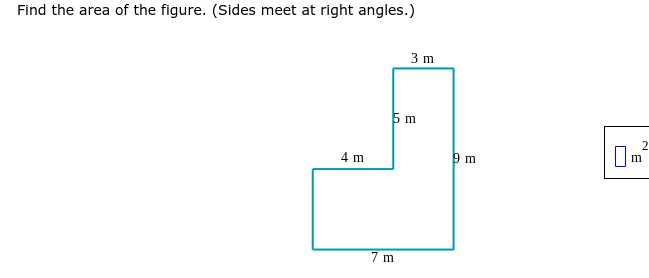
Find the area of the figure. (Sides meet at right angles.)
Understand the Problem
The question is asking us to calculate the area of a given figure composed of various rectangular sections, where sides meet at right angles. To solve this, we will identify the dimensions of each rectangle and sum their areas.
Answer
The area of the figure is $70 \, m^2$.
Answer for screen readers
The area of the figure is $70 , m^2$.
Steps to Solve
- Identify Rectangular Sections
Divide the figure into identifiable rectangular sections. The given figure can be divided into three rectangles:
- Rectangle A (bottom rectangle): 7 m wide and 4 m tall
- Rectangle B (the vertical rectangle on the right): 3 m wide and 9 m tall
- Rectangle C (top rectangle): 3 m wide and 5 m tall
- Calculate Areas of Each Rectangle
Calculate the area of each rectangle using the area formula for rectangles, $Area = width \times height$.
-
Area of Rectangle A: $$ A_A = 7 , m \times 4 , m = 28 , m^2 $$
-
Area of Rectangle B: $$ A_B = 3 , m \times 9 , m = 27 , m^2 $$
-
Area of Rectangle C: $$ A_C = 3 , m \times 5 , m = 15 , m^2 $$
- Sum the Areas
Add the areas of all rectangles to find the total area of the figure.
$$ A_{total} = A_A + A_B + A_C $$
Substituting the area values:
$$ A_{total} = 28 , m^2 + 27 , m^2 + 15 , m^2 $$
- Final Calculation
Calculate the total area:
$$ A_{total} = 28 + 27 + 15 = 70 , m^2 $$
The area of the figure is $70 , m^2$.
More Information
The calculation of the area involved breaking down the figure into simpler rectangular shapes, which can often make complex geometrical problems easier to solve. This method is useful for various applications in architecture, landscaping, and design.
Tips
- Forgetting to add up the areas of all sections. Always double-check each area calculated.
- Mislabeling dimensions or forgetting to correctly identify the width and height for each rectangle, which can lead to incorrect area calculations.
AI-generated content may contain errors. Please verify critical information