Find each of the following in its simplest form: 1) (3/5)^3, 2) (-7)^4, 3) (9/4) x (2/3)^2, 4) 2 * (7/9) ÷ (-1 2/3)^2, 5) (-2/5)^2 x (-5/2)^3, 6) (-2)^4 + (-3)^3.
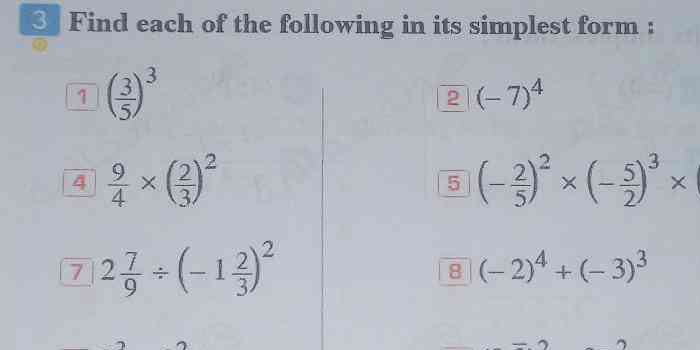
Understand the Problem
The question is asking to simplify a series of expressions involving fractions and exponents. Each expression needs to be simplified to its simplest form, using rules of arithmetic and exponents.
Answer
1) \(\frac{27}{125}\), 2) \(2401\), 3) \(1\), 4) \(\frac{14}{25}\), 5) \(-\frac{5}{2}\), 6) \(-11\)
Answer for screen readers
- (\frac{27}{125})
- (2401)
- (1)
- (\frac{14}{25})
- (-\frac{5}{2})
- (-11)
Steps to Solve
- Simplify ((\frac{3}{5})^3)
To simplify ((\frac{3}{5})^3), we need to cube both the numerator and the denominator:
$$ \left(\frac{3}{5}\right)^3 = \frac{3^3}{5^3} = \frac{27}{125} $$
- Calculate ((-7)^4)
Calculating the fourth power of (-7):
$$ (-7)^4 = 7^4 = 2401 $$
- Simplify ((\frac{9}{4}) \times (\frac{2}{3})^2)
First, calculate ((\frac{2}{3})^2):
$$ \left(\frac{2}{3}\right)^2 = \frac{2^2}{3^2} = \frac{4}{9} $$
Now, multiply by (\frac{9}{4}):
$$ \frac{9}{4} \times \frac{4}{9} = 1 $$
- Calculate (2 \times (\frac{7}{9}) \div (-\frac{5}{3})^2)
First, calculate ((-1 \frac{2}{3})^2):
Convert mixed number (-1 \frac{2}{3}) to an improper fraction:
$$ -\frac{5}{3} = -\frac{5}{3} $$
Then square it:
$$ \left(-\frac{5}{3}\right)^2 = \frac{25}{9} $$
Now the expression becomes:
$$ 2 \times \frac{7}{9} \div \frac{25}{9} = 2 \times \frac{7}{9} \times \frac{9}{25} = \frac{14}{25} $$
- Simplify ((-2/5)^2 \times (-5/2)^3)
First, calculate ((-2/5)^2):
$$ \left(-\frac{2}{5}\right)^2 = \frac{4}{25} $$
Now calculate ((-5/2)^3):
$$ \left(-\frac{5}{2}\right)^3 = -\frac{125}{8} $$
Now multiply both results together:
$$ \frac{4}{25} \times -\frac{125}{8} = -\frac{500}{200} = -\frac{5}{2} $$
- Calculate ((-2)^4 + (-3)^3)
Calculate ((-2)^4):
$$ (-2)^4 = 16 $$
Now calculate ((-3)^3):
$$ (-3)^3 = -27 $$
Now add both results together:
$$ 16 + (-27) = -11 $$
- (\frac{27}{125})
- (2401)
- (1)
- (\frac{14}{25})
- (-\frac{5}{2})
- (-11)
More Information
Each expression was simplified using fundamental rules of exponents, multiplication, and addition of fractions. This emphasizes the importance of understanding fractional and exponential operations.
Tips
- Confusing the signs when raising to even or odd powers, especially for negative numbers.
- Not correctly converting mixed numbers to improper fractions before calculations.
- Misapplying the rules of multiplication and division for fractions.
AI-generated content may contain errors. Please verify critical information