Find all real and imaginary solutions to the equation x^3 + 4x^2 - 15x - 60 = 0.
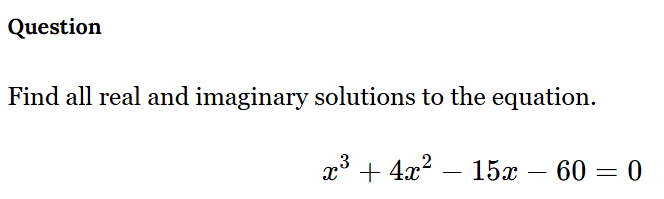
Understand the Problem
The question is asking to find all solutions, both real and imaginary, for the given cubic equation. This involves solving for the roots of the polynomial, which may require techniques such as factoring or using the cubic formula.
Answer
The solutions are \( x = -4, \quad x = \sqrt{15}, \quad x = -\sqrt{15} \).
Answer for screen readers
The solutions to the equation ( x^3 + 4x^2 - 15x - 60 = 0 ) are:
$$ x = -4, \quad x = \sqrt{15}, \quad x = -\sqrt{15} $$
Steps to Solve
-
Identify potential rational roots Using the Rational Root Theorem, we can determine possible rational roots by taking the factors of the constant term (-60) and the leading coefficient (1). The potential rational roots are: ( \pm 1, \pm 2, \pm 3, \pm 4, \pm 5, \pm 6, \pm 10, \pm 12, \pm 15, \pm 20, \pm 30, \pm 60 ).
-
Test the potential roots We can test these values in the original equation ( x^3 + 4x^2 - 15x - 60 = 0 ) to find actual roots. Starting with ( x = 4 ):
$$ 4^3 + 4(4^2) - 15(4) - 60 = 64 + 64 - 60 - 60 = 8 \quad \text{(not a root)} $$ Testing ( x = -3 ):
$$ (-3)^3 + 4(-3)^2 - 15(-3) - 60 = -27 + 36 + 45 - 60 = -6 \quad \text{(not a root)} $$ Testing ( x = -4 ):
$$ (-4)^3 + 4(-4)^2 - 15(-4) - 60 = -64 + 64 + 60 - 60 = 0 \quad \text{(is a root)} $$
Thus, ( x = -4 ) is a root.
- Perform synthetic division Now, we divide the original polynomial by ( (x + 4) ) using synthetic division:
-4 | 1 4 -15 -60
| -4 0 60
-----------------------
1 0 -15 0
The result is ( x^2 - 15 ).
- Solve the quadratic equation Now we solve the quadratic equation ( x^2 - 15 = 0 ):
$$ x^2 = 15 $$
Taking the square root:
$$ x = \pm \sqrt{15} $$
- Compile all solutions The complete set of solutions to the cubic equation ( x^3 + 4x^2 - 15x - 60 = 0 ) includes the found real solutions:
$$ x = -4, \quad x = \sqrt{15}, \quad x = -\sqrt{15} $$
The solutions to the equation ( x^3 + 4x^2 - 15x - 60 = 0 ) are:
$$ x = -4, \quad x = \sqrt{15}, \quad x = -\sqrt{15} $$
More Information
The solutions consist of one rational root ( -4 ) and two irrational roots ( \sqrt{15} ) and ( -\sqrt{15} ). This polynomial is a cubic, meaning it will have three roots in total, which can be real or complex. In this case, all roots are real.
Tips
- Not testing all rational roots: Always ensure to test all potential roots from the Rational Root Theorem.
- Errors in synthetic division: Be careful with the synthetic division steps to avoid calculation errors.
- Miscalculating square roots: Ensure to find both positive and negative roots while solving quadratics.
AI-generated content may contain errors. Please verify critical information