Find all real and imaginary solutions to the equation x^3 + 2x^2 + 9x + 18 = 0.
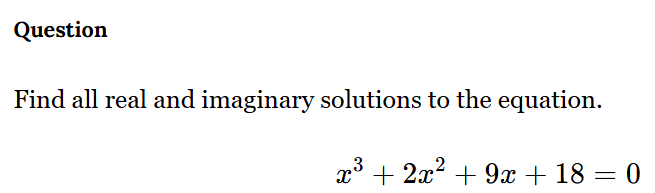
Understand the Problem
The question is asking us to find both real and imaginary solutions to the given polynomial equation. The approach involves identifying the roots of the cubic equation by either factoring or using the quadratic formula for any resulting quadratic components after finding one root.
Answer
The solutions are $x = -2$, $x = 3i$, $x = -3i$.
Answer for screen readers
The real and imaginary solutions are:
- $x = -2$
- $x = 3i$
- $x = -3i$
Steps to Solve
- Identify possible rational roots
Using the Rational Root Theorem, we list the factors of the constant term (18) and the leading coefficient (1). The possible rational roots are $\pm 1, \pm 2, \pm 3, \pm 6, \pm 9, \pm 18$.
- Test potential roots
We will test these values by substituting them into the polynomial $f(x) = x^3 + 2x^2 + 9x + 18$.
- Testing $x = -3$:
$$ f(-3) = (-3)^3 + 2(-3)^2 + 9(-3) + 18 = -27 + 18 - 27 + 18 = -18 \neq 0 $$
- Testing $x = -2$:
$$ f(-2) = (-2)^3 + 2(-2)^2 + 9(-2) + 18 = -8 + 8 - 18 + 18 = 0 $$
Thus, $x = -2$ is a root.
- Factor polynomial using the found root
We can perform polynomial long division of $f(x)$ by $(x + 2)$:
$$ f(x) = (x + 2)(x^2 + 9) $$
- Solve the quadratic factor
Now we need to solve $x^2 + 9 = 0$ to find the imaginary roots.
$$ x^2 = -9 $$
Taking the square root gives:
$$ x = \pm 3i $$
- Summarize all solutions
The solutions to the original equation are $x = -2$, $x = 3i$, and $x = -3i$.
The real and imaginary solutions are:
- $x = -2$
- $x = 3i$
- $x = -3i$
More Information
The equation $x^3 + 2x^2 + 9x + 18 = 0$ is a cubic polynomial. The factored form $(x + 2)(x^2 + 9)$ highlights that one real root exists and that there are coinciding pairs of imaginary roots.
Tips
- Overlooking imaginary roots: Often, students stop searching after finding one real root. It is essential to check the remaining quadratic factor for additional solutions.
- Mistaking the sign when taking square roots: The solutions from $x^2 + 9 = 0$ yield both a positive and a negative imaginary component.
AI-generated content may contain errors. Please verify critical information