Factor u³ + 125 completely.
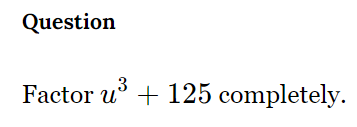
Understand the Problem
The question is asking us to factor the expression u³ + 125 completely. This involves recognizing it as a sum of cubes and applying the appropriate factoring formula.
Answer
The completely factored form of $u^3 + 125$ is: $(u + 5)(u^2 - 5u + 25)$.
Answer for screen readers
The completely factored form of the expression $u^3 + 125$ is: $ (u + 5)(u^2 - 5u + 25) $.
Steps to Solve
- Recognize the Sum of Cubes Formula
The expression $u^3 + 125$ can be seen as a sum of cubes. Recall the sum of cubes factoring formula: $$ a^3 + b^3 = (a + b)(a^2 - ab + b^2) $$
In this case, $a = u$ and $b = 5$ since $125 = 5^3$.
- Identify a and b
Set $a = u$ and $b = 5$. Now we can apply the sum of cubes formula.
- Apply the Formula
Using the formula, we have: $$ u^3 + 125 = (u + 5)(u^2 - u \cdot 5 + 5^2) $$
This simplifies to: $$ u^3 + 125 = (u + 5)(u^2 - 5u + 25) $$
- Final Factorization
Thus, the completely factored form of $u^3 + 125$ is: $$ (u + 5)(u^2 - 5u + 25) $$
The completely factored form of the expression $u^3 + 125$ is: $ (u + 5)(u^2 - 5u + 25) $.
More Information
The expression $u^3 + 125$ can be recognized as a sum of cubes, which is a common form in algebra that can be factored using the sum of cubes formula. This is significant in various areas of mathematics, especially in polynomial factorization.
Tips
- Forgetting the Formula: A common mistake is not recognizing the sum of cubes form. Always check if the expression fits the $a^3 + b^3$ format.
- Incorrectly Identifying b: Ensure you correctly identify $b$ when you rewrite constants as cubes, like recognizing $125$ as $5^3$.
AI-generated content may contain errors. Please verify critical information