Factor the expression completely: x^3y^4 - x^4y^4.
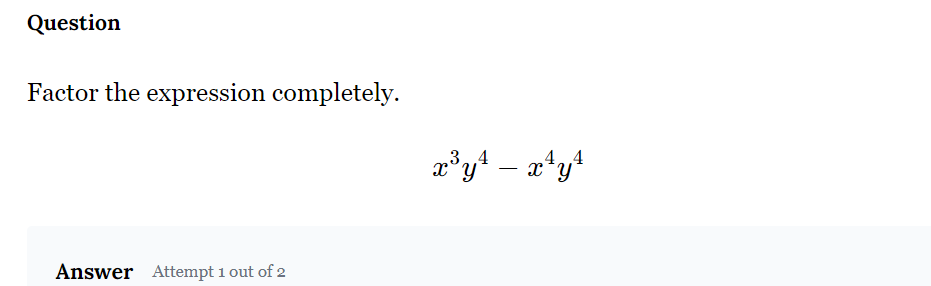
Understand the Problem
The question is asking to factor the expression completely. The expression provided is x^3y^4 - x^4y^4, which suggests using techniques such as factoring out common factors.
Answer
The completely factored expression is \( x^3 y^4 (1 - x) \).
Answer for screen readers
The factored form of the expression is ( x^3 y^4 (1 - x) ).
Steps to Solve
- Identify the common factors
The expression is $x^3 y^4 - x^4 y^4$. We notice that both terms share common factors $x^3$ and $y^4$.
- Factor out the common factors
When we factor out $x^3 y^4$, the expression becomes:
$$ x^3 y^4 (1 - x) $$
- Final expression
The expression $x^3 y^4 (1 - x)$ is now fully factored.
Thus, the complete factorization of the original expression is:
$$ x^3 y^4 (1 - x) $$
The factored form of the expression is ( x^3 y^4 (1 - x) ).
More Information
This expression demonstrates the use of the distributive property in reverse, allowing us to simplify the original expression by extracting common factors.
Tips
- Not identifying all common factors: Ensure to check for common factors in all terms.
- Missing signs when factoring: Double-check the signs to ensure they are retained properly in the factored form.