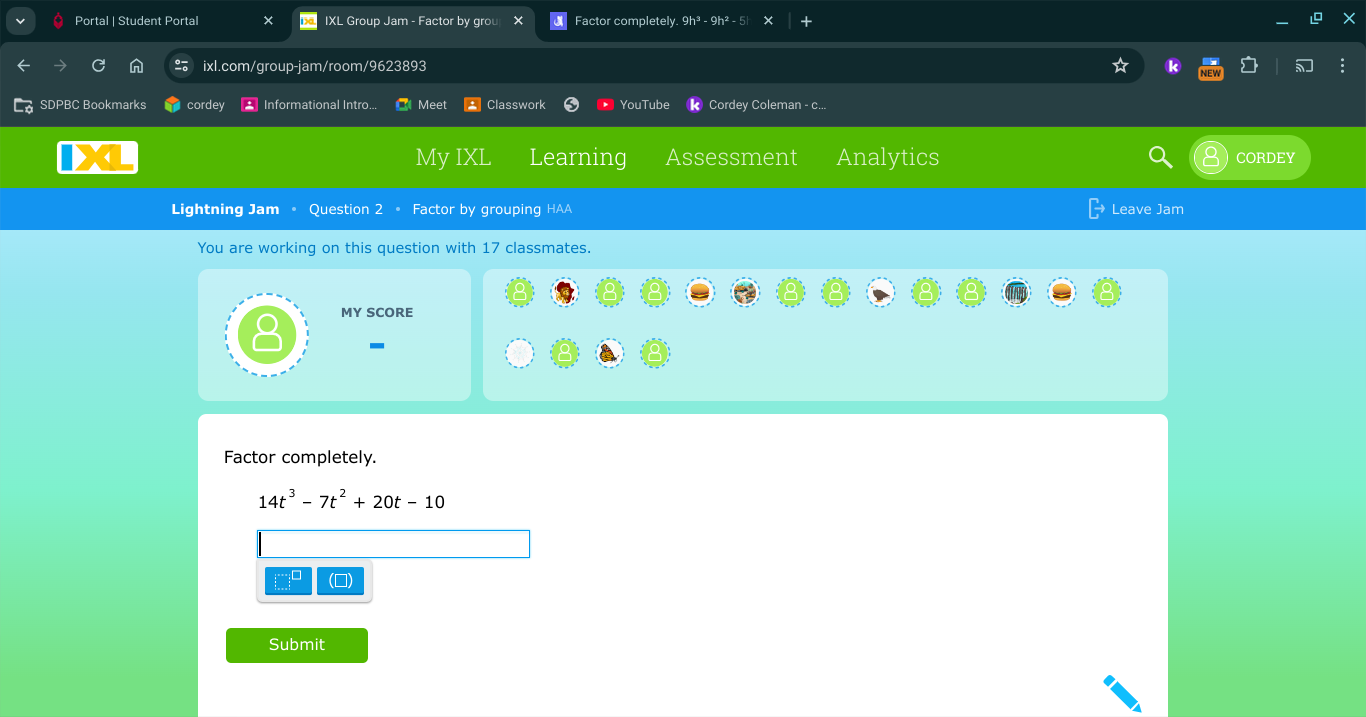
Factor completely. 14t^3 - 7t^2 + 20t - 10
Understand the Problem
The question is asking to factor a polynomial completely. The polynomial given is 14t^3 - 7t^2 + 20t - 10. The goal is to use factoring techniques, such as grouping, to simplify this expression.
Answer
$ (2t - 1)(7t^2 + 10) $
Answer for screen readers
The completely factored form of the polynomial (14t^3 - 7t^2 + 20t - 10) is
$$(2t - 1)(7t^2 + 10)$$
Steps to Solve
- Group the terms First, we can group the polynomial into two pairs:
$$ (14t^3 - 7t^2) + (20t - 10) $$
- Factor out common factors from each group Now, factor out the greatest common factors from each grouped part.
From the first group (14t^3 - 7t^2):
- The common factor is (7t^2), so we have:
$$ 7t^2(2t - 1) $$
From the second group (20t - 10):
- The common factor is (10), so we have:
$$ 10(2t - 1) $$
So now, our expression looks like:
$$ 7t^2(2t - 1) + 10(2t - 1) $$
- Factor out the common binomial Now, notice that ((2t - 1)) is common in both groups. Factor this out:
$$ (2t - 1)(7t^2 + 10) $$
- Final expression The completely factored form of the polynomial is:
$$ (2t - 1)(7t^2 + 10) $$
The completely factored form of the polynomial (14t^3 - 7t^2 + 20t - 10) is
$$(2t - 1)(7t^2 + 10)$$
More Information
Factoring by grouping is a useful technique when a polynomial has four terms. In this polynomial, you can see how grouping helped isolate common factors effectively, leading to a simplified form.
Tips
- Forgetting to factor out the greatest common factor from each group, leading to incorrect intermediate steps.
- Not recognizing a common binomial factor, which prevents reaching the most simplified form.
AI-generated content may contain errors. Please verify critical information