8(x - 3)/2 + 5x = 9(x - 1) - 3
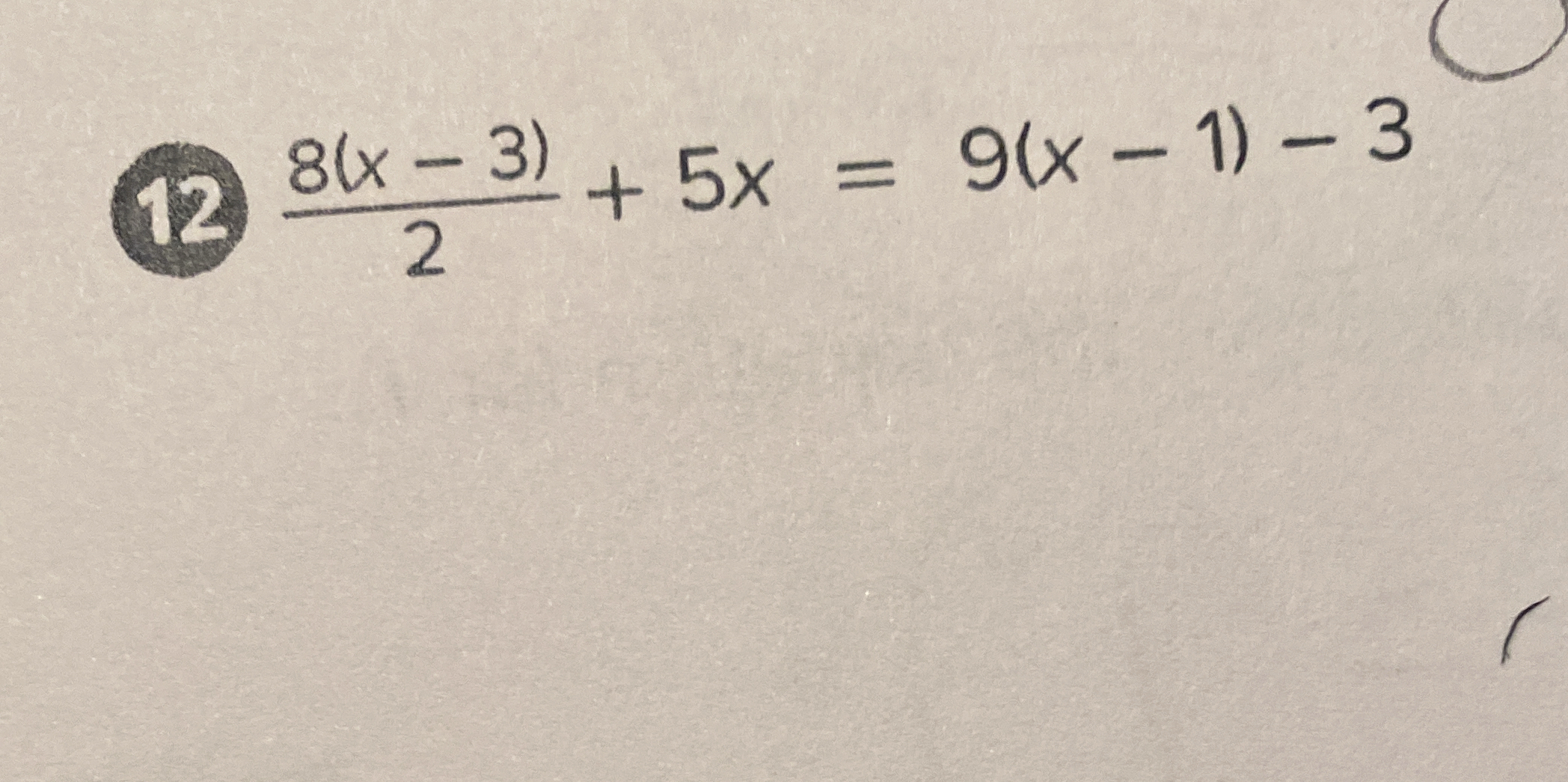
Understand the Problem
The question is asking to solve an equation involving the variables x and constants, represented in a mathematical format. The challenge is to isolate x and find its value.
Answer
Any value of $x$ satisfies the equation.
Answer for screen readers
The solution is that any value of $x$ satisfies the equation.
Steps to Solve
- Distribute the terms inside the parentheses
First, distribute the $8$ and $9$ in their respective terms.
For the left side: $$ 8(x - 3) = 8x - 24 $$
For the right side: $$ 9(x - 1) = 9x - 9 $$
- Rewrite the equation with distributed terms
Now rewrite the entire equation with the distributed terms: $$ \frac{8x - 24}{2} + 5x = 9x - 9 - 3 $$
- Simplify each side
Simplify the left side by dividing $8x - 24$ by $2$: $$ \frac{8x}{2} - \frac{24}{2} = 4x - 12 $$ So, now the equation is: $$ 4x - 12 + 5x = 9x - 12 $$
- Combine like terms
Combine like terms on the left side: $$ (4x + 5x - 12) = (9x - 12) $$ This simplifies to: $$ 9x - 12 = 9x - 12 $$
- Analyze the result
Notice that both sides are equal, which indicates that: $$ 0 = 0 $$ This means any value for $x$ satisfies the equation.
The solution is that any value of $x$ satisfies the equation.
More Information
Since the equation simplifies to $0 = 0$, it indicates infinite solutions. This usually means that the equation represents a true statement independent of the value of $x$.
Tips
- Forgetting to distribute correctly inside the parentheses can lead to incorrect terms.
- Not simplifying the equation properly can make it appear that there are no solutions.
AI-generated content may contain errors. Please verify critical information