Express the equation 2t^{-10} - 3t^{-5} + 1 = 0 in terms of x where x = 1/t^5.
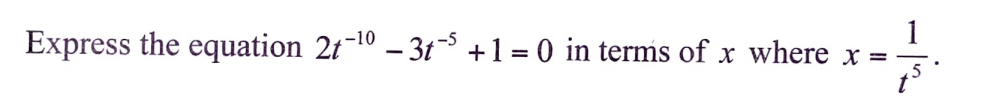
Understand the Problem
The question is asking to transform the given equation into a form that uses the variable x, which is defined as the reciprocal of t raised to the fifth power. This involves substituting and manipulating the equation accordingly.
Answer
The equation expressed in terms of \( x \) is $$ 2x^2 - 3x + 1 = 0 $$
Answer for screen readers
The transformed equation in terms of ( x ) is
$$ 2x^2 - 3x + 1 = 0 $$
Steps to Solve
- Identify the relationship between variables
We start with the substitution for ( x ). Given ( x = \frac{1}{t^5} ), we can express ( t ) in terms of ( x ):
$$ t^5 = \frac{1}{x} \implies t = \left(\frac{1}{x}\right)^{\frac{1}{5}} $$
- Express ( t^{-10} ) and ( t^{-5} ) in terms of ( x )
Using the substitution ( t = \left(\frac{1}{x}\right)^{\frac{1}{5}} ):
- For ( t^{-10} ):
$$ t^{-10} = \left(\left(\frac{1}{x}\right)^{\frac{1}{5}}\right)^{-10} = \left(\frac{1}{x}\right)^{-\frac{10}{5}} = x^2 $$
- For ( t^{-5} ):
$$ t^{-5} = \left(\left(\frac{1}{x}\right)^{\frac{1}{5}}\right)^{-5} = \left(\frac{1}{x}\right)^{-1} = x $$
- Substitute into the original equation
Now we substitute ( t^{-10} ) and ( t^{-5} ) back into the equation:
$$ 2t^{-10} - 3t^{-5} + 1 = 0 $$
This turns into:
$$ 2x^2 - 3x + 1 = 0 $$
The transformed equation in terms of ( x ) is
$$ 2x^2 - 3x + 1 = 0 $$
More Information
This equation is a quadratic in ( x ). Solving it can reveal the values of ( x ) that correspond to the original equation in terms of ( t ). The solution can be used in various applications, like finding roots or analyzing the behavior of functions.
Tips
- Neglecting to correctly transform powers: Ensure you properly manage the exponents when substituting ( t ) with ( x ).
- Incorrectly factoring the quadratic: Be careful in the factorization process; always check by multiplying back to verify.
AI-generated content may contain errors. Please verify critical information