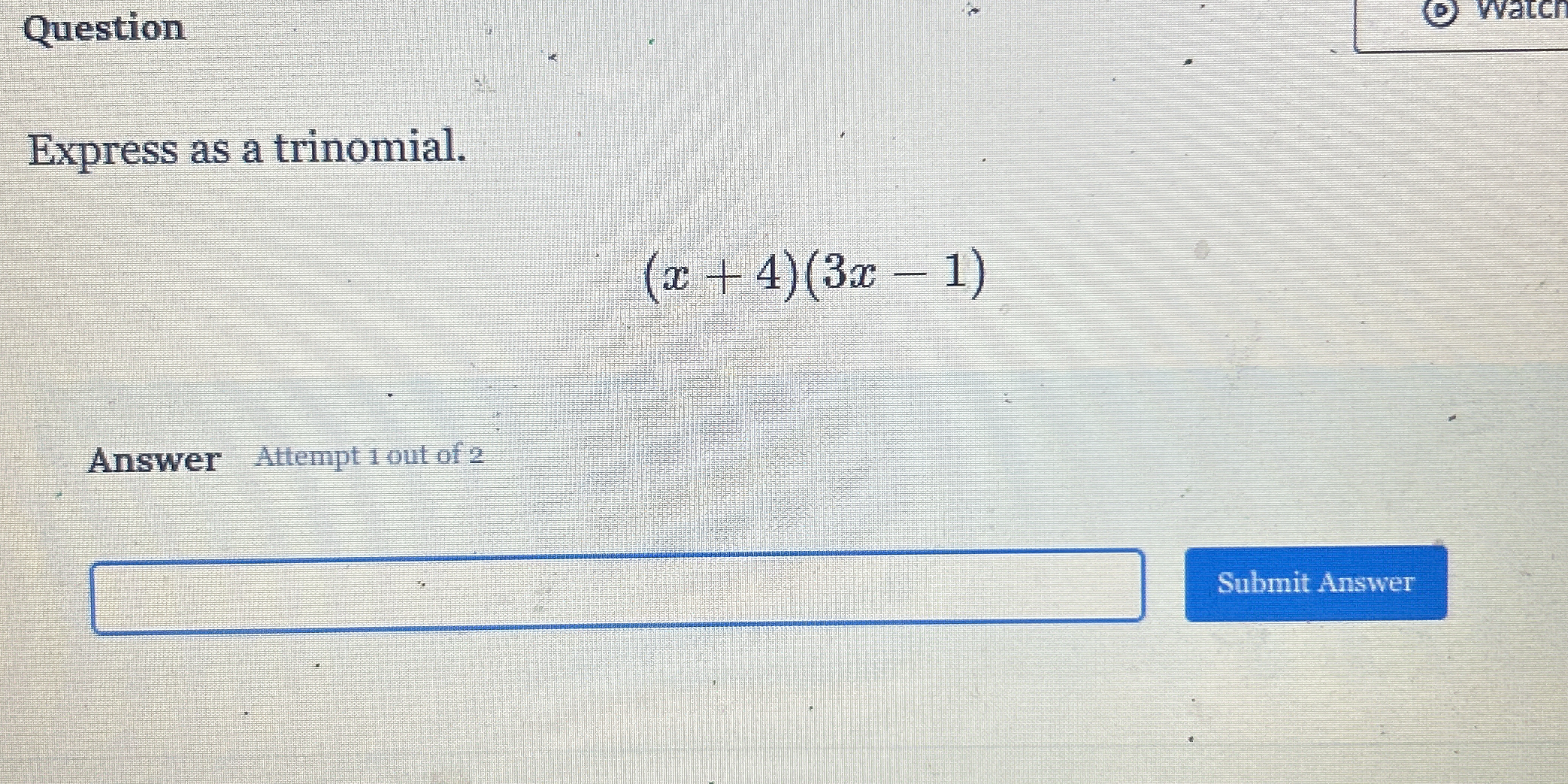
Express as a trinomial: (x + 4)(3x - 1)
Understand the Problem
The question is asking to express the product of the two binomials (x + 4)(3x - 1) as a single trinomial by multiplying the two expressions together.
Answer
$3x^2 + 11x - 4$
Answer for screen readers
The trinomial is $3x^2 + 11x - 4$.
Steps to Solve
-
Write Down the Expression We have the expression $(x + 4)(3x - 1)$.
-
Distribute Each Term We need to use the distributive property (also known as the FOIL method for binomials). Distribute each term in the first bracket to each term in the second bracket:
- First: $x \cdot 3x$
- Outer: $x \cdot (-1)$
- Inner: $4 \cdot 3x$
- Last: $4 \cdot (-1)$
-
Calculate Each Product Now, perform the calculations for each part:
- First: $x \cdot 3x = 3x^2$
- Outer: $x \cdot (-1) = -x$
- Inner: $4 \cdot 3x = 12x$
- Last: $4 \cdot (-1) = -4$
-
Combine Like Terms Now combine all the terms together: $$ 3x^2 - x + 12x - 4 $$
-
Simplify the Expression Combine the like terms, which are $-x$ and $12x$: $$ 3x^2 + (12x - x) - 4 = 3x^2 + 11x - 4 $$
The trinomial is $3x^2 + 11x - 4$.
More Information
The result $3x^2 + 11x - 4$ is in standard form, where the highest degree term is first. This method of multiplying binomials is useful in algebra for simplifying expressions and solving equations.
Tips
- Forgetting to combine like terms can lead to an incorrect final expression. Make sure to carefully group and add similar terms.
- Not applying the distributive property correctly may result in missing some products. Always ensure each term from the first binomial is multiplied by each term in the second.
AI-generated content may contain errors. Please verify critical information