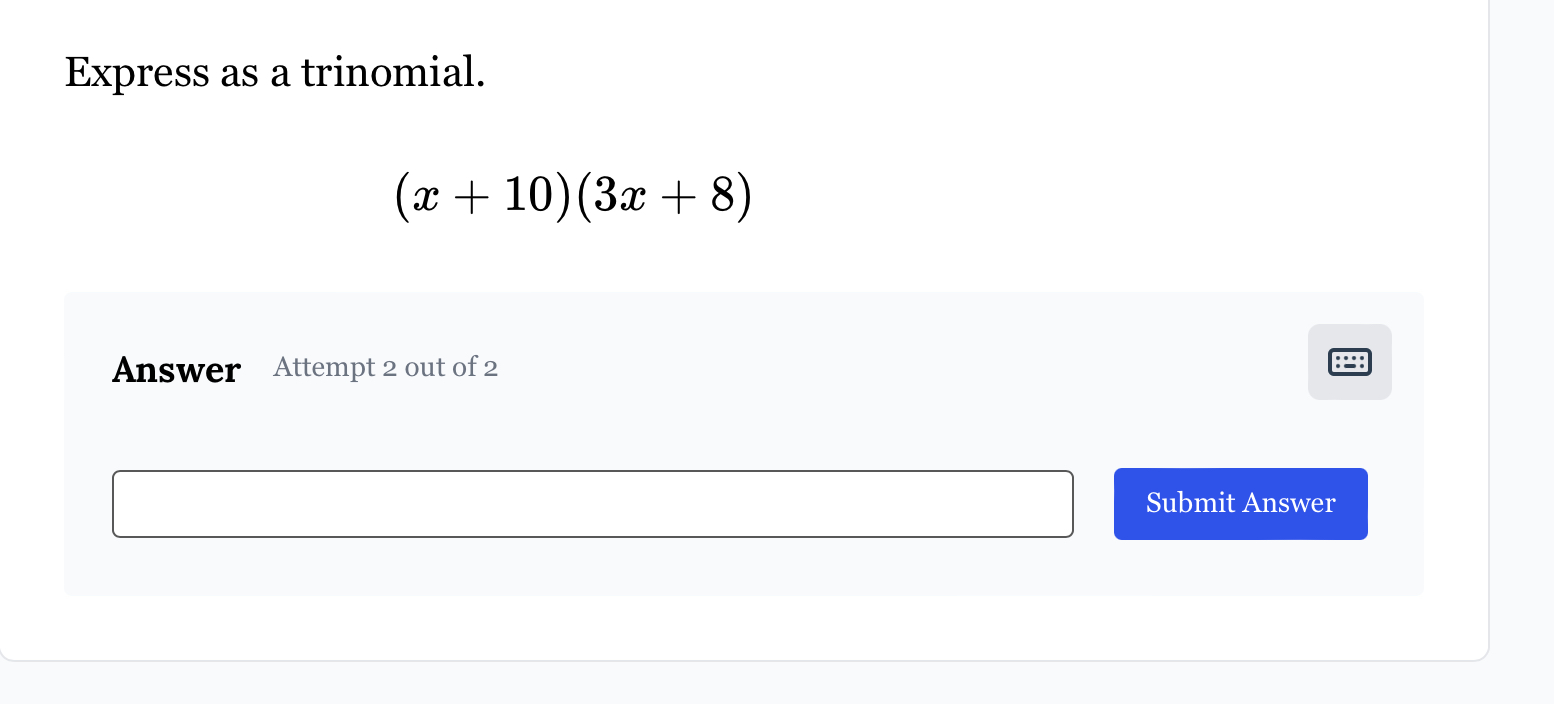
Express as a trinomial: (x + 10)(3x + 8)
Understand the Problem
The question is asking to express the product of two binomials, (x + 10) and (3x + 8), as a trinomial. This involves applying the distributive property or FOIL method to simplify the expression.
Answer
The expanded trinomial is \( 3x^2 + 38x + 80 \).
Answer for screen readers
The product of the binomials ( (x + 10)(3x + 8) ) expressed as a trinomial is ( 3x^2 + 38x + 80 ).
Steps to Solve
- Identify the binomials
We have the binomials ( (x + 10) ) and ( (3x + 8) ).
- Apply the FOIL method
Use the FOIL (First, Outside, Inside, Last) method to multiply the two binomials:
-
First: Multiply the first terms:
( x \cdot 3x = 3x^2 ) -
Outside: Multiply the outside terms:
( x \cdot 8 = 8x ) -
Inside: Multiply the inside terms:
( 10 \cdot 3x = 30x ) -
Last: Multiply the last terms:
( 10 \cdot 8 = 80 )
- Combine the results
Now, combine all these results: $$ 3x^2 + 8x + 30x + 80 $$
- Simplify the expression
Combine like terms ((8x + 30x)): $$ 3x^2 + 38x + 80 $$
The product of the binomials ( (x + 10)(3x + 8) ) expressed as a trinomial is ( 3x^2 + 38x + 80 ).
More Information
This trinomial represents the expanded form of the product of the two binomials. The coefficients and constants indicate the contributions from each term in the original binomials when multiplied.
Tips
- Forgetting to add like terms correctly. Always check that all like terms (terms with the same variable and exponent) are combined properly.
- Not applying the FOIL method correctly. Ensure that all four products (First, Outside, Inside, Last) are calculated before combining them.
AI-generated content may contain errors. Please verify critical information