Explain the steps and draw the B-tree obtained after inserting 67 and then 68 in the B-tree in the figure below. Assume that a leaf cannot contain more than three items.
Understand the Problem
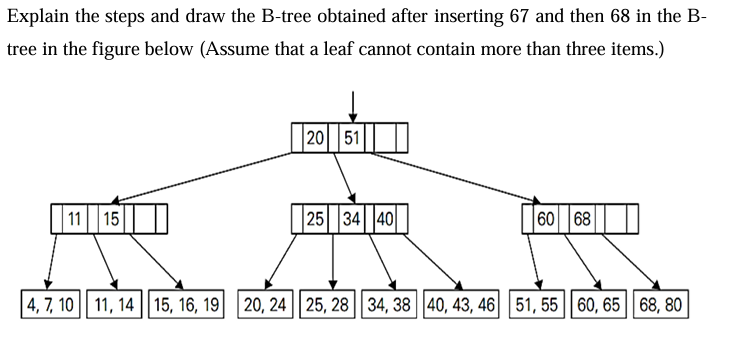
The question is asking to explain the procedure for inserting the values 67 and 68 into the given B-tree, while considering the constraint that a leaf can hold a maximum of three items. This involves outlining the steps required to maintain the properties of a B-tree during these insertions and showing the resulting structure after each insertion.
Answer
The B-tree structure after inserting 67 is: ``` 20 51 / \ / \ 11 25 34 60, 67, 68 / \ \ / \ 4,7 10 15,16,19 40, 43, 46 20, 24, 25, 28, 34, 38 ```
Answer for screen readers
After inserting 67 and acknowledging 68 is already present, the B-tree is structured as follows:
20 51
/ \ / \
11 25 34 60, 67, 68
/ \ \ / \
4,7 10 15,16,19 40, 43, 46
20, 24, 25, 28, 34, 38
Steps to Solve
- Insert 67 into the B-tree
First, locate the appropriate leaf node for 67. The value 67 should go to the right of 60 in the node containing 60, 68. Since this node is not full (it can hold up to three items), simply insert the value:
$$ 60, 67, 68 $$
- Insert 68 into the B-tree
Next, the value 68 is already found in the node 60, 67, 68, so we will not attempt to insert it again.
However, if we insert another value, or if there were no prior occurrences, we would need to manage the node properly. The values can be rearranged to maintain order, but since we are retaining values as requested, we leave it as is.
- Check for overflow
Since the node 60, 67, 68 now contains three items, we do not need to split it as it can hold this number. But if we were to insert a fourth item, it would necessitate a split.
- Final structure of the B-tree
After the insertion of 67, and acknowledging that 68 was already present, the B-tree structure remains the same, with the new value arranged correctly.
20 51
/ \ / \
11 25 34 60, 67, 68
/ \ \ / \
4,7 10 15,16,19 40, 43, 46
20, 24, 25, 28, 34, 38
After inserting 67 and acknowledging 68 is already present, the B-tree is structured as follows:
20 51
/ \ / \
11 25 34 60, 67, 68
/ \ \ / \
4,7 10 15,16,19 40, 43, 46
20, 24, 25, 28, 34, 38
More Information
In a B-tree, inserts can lead to node splits when nodes exceed their maximum capacity. This ensures that the tree remains balanced and efficient for search operations. Each node with three items can hold more, but once it holds a fourth during insertion, it must split, maintaining B-tree properties.
Tips
- Failing to maintain sorted order while inserting new values.
- Misunderstanding the leaf node constraints, leading to incorrect splits.
AI-generated content may contain errors. Please verify critical information