Expand the expression to a polynomial in standard form: (-x - 10)(x^2 - 2x + 1)
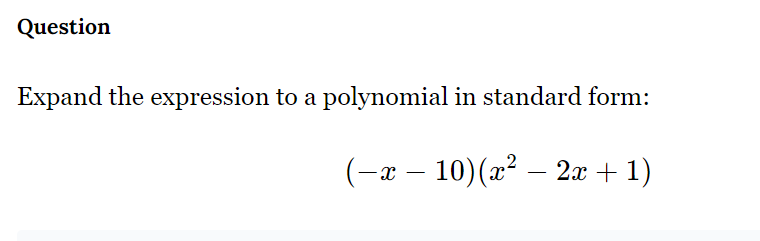
Understand the Problem
The question is asking us to expand the given expression, which is the product of two polynomials, into standard polynomial form. This involves distributing each term in the first polynomial to every term in the second polynomial and then combining like terms.
Answer
The expanded polynomial is $$ -x^3 - 8x^2 + 19x - 10 $$.
Answer for screen readers
The expanded polynomial in standard form is: $$ -x^3 - 8x^2 + 19x - 10 $$
Steps to Solve
-
Distribute the first term Begin by distributing $-x$ to each term in the second polynomial ($x^2 - 2x + 1$): [ -x \cdot x^2 = -x^3 ] [ -x \cdot (-2x) = 2x^2 ] [ -x \cdot 1 = -x ]
-
Distribute the second term Next, distribute $-10$ to each term in the second polynomial: [ -10 \cdot x^2 = -10x^2 ] [ -10 \cdot (-2x) = 20x ] [ -10 \cdot 1 = -10 ]
-
Combine like terms Now, combine all the results from both distributions: [ -x^3 + 2x^2 - x - 10x^2 + 20x - 10 ] Combine the like terms:
- For $x^2$: $2x^2 - 10x^2 = -8x^2$
- For $x$: $-x + 20x = 19x$
- Write in standard form Putting it all together, we write the polynomial in standard form: [ -x^3 - 8x^2 + 19x - 10 ]
The expanded polynomial in standard form is: $$ -x^3 - 8x^2 + 19x - 10 $$
More Information
Expanding polynomials is a fundamental skill in algebra. It helps in understanding how to manipulate polynomial expressions, which is essential for solving equations and analyzing functions.
Tips
- Forgetting to distribute all terms: Ensure you distribute every term in the first polynomial across all terms in the second polynomial.
- Miscombining like terms: When combining terms, pay attention to the signs and coefficients.
AI-generated content may contain errors. Please verify critical information