Expand the expression to a polynomial in standard form: (3x + 1)(3x^2 + 7x - 7)
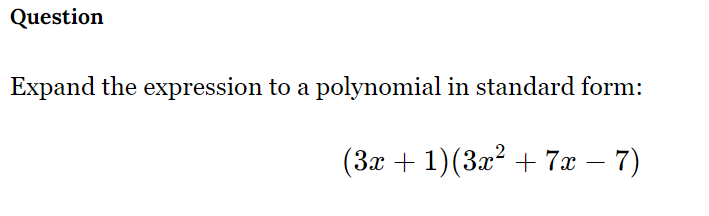
Understand the Problem
The question is asking us to expand the given expression by multiplying the two polynomials and then simplifying it into standard form. This involves using the distributive property to combine like terms.
Answer
The final expanded polynomial is \(9x^3 + 24x^2 - 14x - 7\).
Answer for screen readers
The expanded polynomial in standard form is:
$$ 9x^3 + 24x^2 - 14x - 7 $$
Steps to Solve
- Distributing the first term
Start by distributing the first term of the first polynomial, (3x), to each term in the second polynomial:
$$ 3x \cdot 3x^2 = 9x^3 $$ $$ 3x \cdot 7x = 21x^2 $$ $$ 3x \cdot (-7) = -21x $$
So, from (3x(3x^2 + 7x - 7)), we get (9x^3 + 21x^2 - 21x).
- Distributing the second term
Now, distribute the second term of the first polynomial, (1), to each term in the second polynomial:
$$ 1 \cdot 3x^2 = 3x^2 $$ $$ 1 \cdot 7x = 7x $$ $$ 1 \cdot (-7) = -7 $$
From (1(3x^2 + 7x - 7)), we obtain (3x^2 + 7x - 7).
- Combining all terms
Combine all the results from the distributions:
$$ 9x^3 + 21x^2 - 21x + 3x^2 + 7x - 7 $$
- Combining like terms
Now group the like terms:
- The (x^3) terms: (9x^3)
- The (x^2) terms: (21x^2 + 3x^2 = 24x^2)
- The (x) terms: (-21x + 7x = -14x)
- The constant term: (-7)
Thus, the expression simplifies to:
$$ 9x^3 + 24x^2 - 14x - 7 $$
The expanded polynomial in standard form is:
$$ 9x^3 + 24x^2 - 14x - 7 $$
More Information
In expanding polynomials, the distributive property allows us to effectively multiply every term in one polynomial by every term in another polynomial. This process is fundamental in algebra and is essential for polynomial functions.
Tips
- Forgetting to distribute all terms properly, leading to missing terms.
- Not combining like terms after the distributions.
- Misplacing the sign when dealing with negative numbers.