Expand (9 * (x^x / (1 + 2^x)))
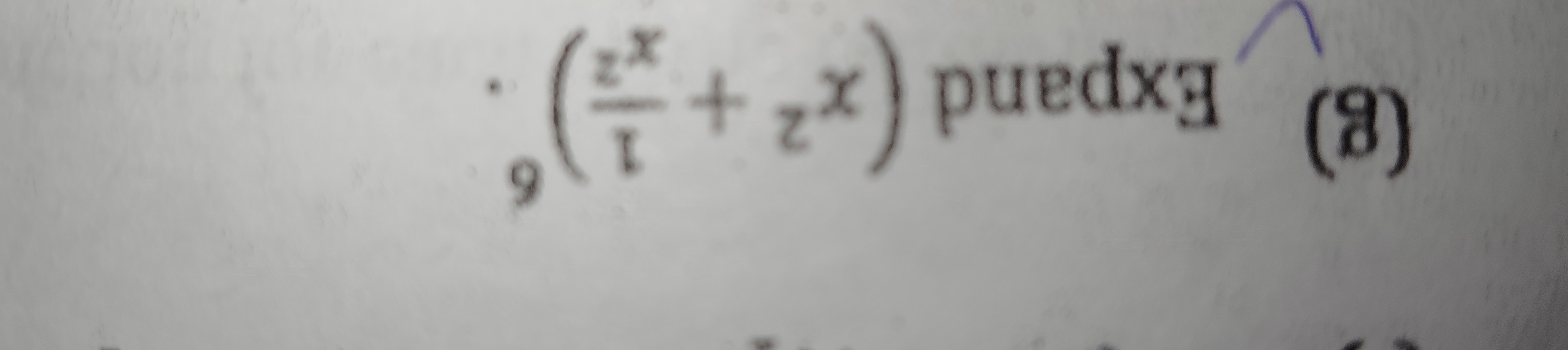
Understand the Problem
The question appears to be related to expanding a mathematical expression. Specifically, it looks like a request to expand the expression inside the parentheses, which includes a fraction involving powers of x.
Answer
The expanded expression is $ \frac{9x^x}{1 + 2^x} $.
Answer for screen readers
The expanded expression is: $$ \frac{9x^x}{1 + 2^x} $$
Steps to Solve
-
Expand the expression Start with the expression: $$ 9 \cdot \left(\frac{x^x}{1 + 2^x}\right) $$ Distributing the 9 gives: $$ \frac{9x^x}{1 + 2^x} $$
-
Identify the structure of the expression The new expression can be analyzed as a fraction where the numerator is $9x^x$ and the denominator is $1 + 2^x$.
-
Rewrite the expression The expression now stands as: $$ \frac{9x^x}{1 + 2^x} $$ This can help in further simplification if needed, but as it stands, it's already quite expanded.
The expanded expression is: $$ \frac{9x^x}{1 + 2^x} $$
More Information
This expression represents the multiplication of 9 with the fraction $\frac{x^x}{1 + 2^x}$. It can be useful in various contexts in calculus or algebra, especially when analyzing functions.
Tips
- Forgetting to distribute the multiplication across the fraction.
- Not properly simplifying the expressions after expansion. Ensure to rewrite the fraction clearly.
AI-generated content may contain errors. Please verify critical information