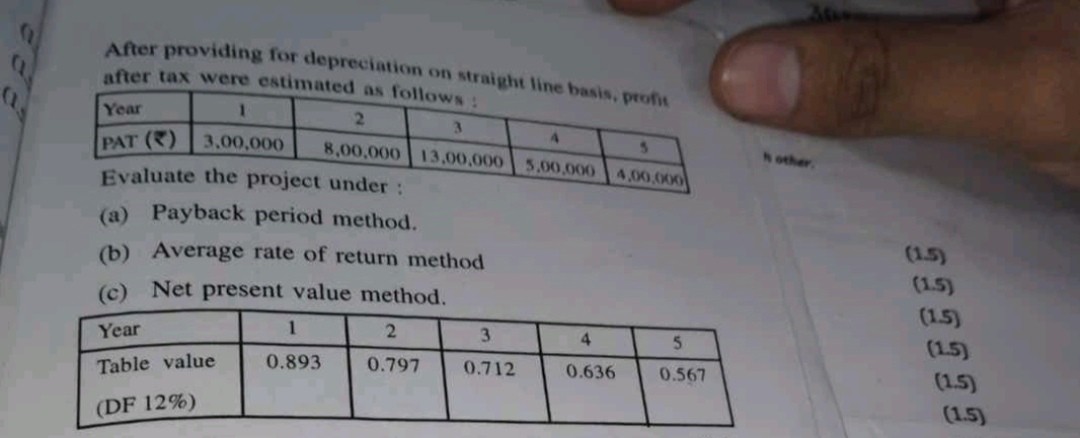
Evaluate the project under: (a) Payback period method. (b) Average rate of return method. (c) Net present value method.

Understand the Problem

The question is asking to evaluate a project based on three different financial assessment methods: payback period method, average rate of return method, and net present value method using provided profit after tax (PAT) figures and discount factors (DF).

Answer

Payback Period: 3.2 years, ARR: 26.4%, NPV: ₹-1,24,100.

Steps to Solve

Calculate Payback Period

The payback period is the time required to recover the initial investment. For this calculation, we assume an initial investment of ₹25,00,000 (based on the sum of profits).
- Cumulative cash flow for each year:
  - Year 1: ₹3,00,000
  - Year 2: ₹3,00,000 + ₹8,00,000 = ₹11,00,000
  - Year 3: ₹11,00,000 + ₹13,00,000 = ₹24,00,000
  - Year 4: ₹24,00,000 + ₹5,00,000 = ₹29,00,000
The payback period occurs between Year 3 and Year 4.

Calculation for exact payback in Year 4: $$ \text{Payback Time} = 3 + \frac{\text{Remaining to recover}}{\text{Cash flow in Year 4}} $$ $$ = 3 + \frac{1,00,000}{5,00,000} = 3 + 0.2 = 3.2 \text{ years} $$
Calculate Average Rate of Return (ARR)

The ARR is calculated using the average annual profit and the initial investment.
- Total profit over 5 years: $$ \text{Total PAT} = 3,00,000 + 8,00,000 + 13,00,000 + 5,00,000 + 4,00,000 = 33,00,000 $$
- Average annual profit: $$ \text{Average Annual PAT} = \frac{33,00,000}{5} = 6,60,000 $$
- ARR Formula: $$ \text{ARR} = \left( \frac{\text{Average Profit}}{\text{Initial Investment}} \right) \times 100 $$ $$ = \left( \frac{6,60,000}{25,00,000} \right) \times 100 = 26.4% $$
Calculate Net Present Value (NPV)

NPV is calculated by discounting the cash flows using the provided discount factors.
- NPV calculation: $$ \text{NPV} = \sum (\text{PAT in Year n} \times \text{DF for Year n}) - \text{Initial Investment} $$
- Calculate each year's contribution:
- Year 1: $$ 3,00,000 \times 0.893 = 2,67,900 $$
- Year 2: $$ 8,00,000 \times 0.797 = 6,37,600 $$
- Year 3: $$ 13,00,000 \times 0.712 = 9,25,600 $$
- Year 4: $$ 5,00,000 \times 0.636 = 3,18,000 $$
- Year 5: $$ 4,00,000 \times 0.567 = 2,26,800 $$
- Total discounted cash flow: $$ \text{Total Discounted Cash Flow} = 2,67,900 + 6,37,600 + 9,25,600 + 3,18,000 + 2,26,800 = 23,75,900 $$
- NPV: $$ \text{NPV} = 23,75,900 - 25,00,000 = -1,24,100 $$

Payback Period: 3.2 years
Average Rate of Return (ARR): 26.4%
Net Present Value (NPV): ₹-1,24,100

More Information

These calculations indicate that while the project has a reasonable payback period and a high ARR, the negative NPV suggests that it may not be a worthwhile investment at a 12% discount rate.

Tips

Forgetting to subtract the initial investment when calculating NPV can lead to inaccurate conclusions.
Incorrectly calculating cumulative cash flows can misrepresent the payback period.
Not using the correct discount factors for each year can affect the NPV accuracy.

AI-generated content may contain errors. Please verify critical information

Thank you for voting!