Evaluate the integral ∫ x^(2/3) √x dx.
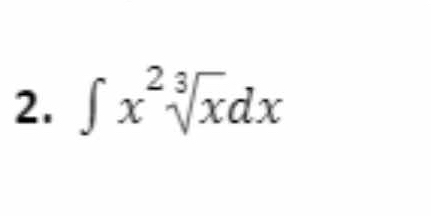
Understand the Problem
The question is asking for the evaluation of the integral ∫ x^(2/3) √x dx, which involves finding the antiderivative of the given expression.
Answer
$$ \frac{6}{13} x^{13/6} + C $$
Answer for screen readers
The evaluated integral is
$$ \frac{6}{13} x^{13/6} + C $$
Steps to Solve
- Rewrite the Integral
First, we will rewrite the integral in a simpler form. The square root function can be represented as an exponent.
The integral becomes:
$$ \int x^{2/3} x^{1/2} , dx $$
- Combine the Exponents
Next, we need to combine the exponents. We can use the property of exponents that states $a^m a^n = a^{m+n}$.
Adding the exponents:
$$ \int x^{2/3 + 1/2} , dx $$
To add ( \frac{2}{3} ) and ( \frac{1}{2} ), we find a common denominator:
$$ \frac{2}{3} = \frac{4}{6}, \quad \frac{1}{2} = \frac{3}{6} $$
Thus,
$$ 2/3 + 1/2 = \frac{4}{6} + \frac{3}{6} = \frac{7}{6} $$
So we have:
$$ \int x^{7/6} , dx $$
- Integrate
Now we can find the antiderivative using the power rule for integration, which states:
$$ \int x^n , dx = \frac{x^{n+1}}{n+1} + C $$
Applying the rule here:
$$ \int x^{7/6} , dx = \frac{x^{7/6 + 1}}{7/6 + 1} + C $$
First, calculate ( 7/6 + 1 ):
$$ 7/6 + 1 = \frac{7}{6} + \frac{6}{6} = \frac{13}{6} $$
Thus, the integral becomes:
$$ \frac{x^{13/6}}{13/6} + C $$
This can be simplified further:
$$ = \frac{6}{13} x^{13/6} + C $$
The evaluated integral is
$$ \frac{6}{13} x^{13/6} + C $$
More Information
This integral showcases the combination of exponents and the power rule for integration. It's a good example of how to manipulate expressions for easier integration.
Tips
- Confusing when to apply the power rule: Ensure you always increase the exponent by 1 before dividing.
- Mistaking the square root exponent: Remember that ( \sqrt{x} = x^{1/2} ).
AI-generated content may contain errors. Please verify critical information