Evaluate the integral of (x^2 + 4x + 2) / (6x) dx
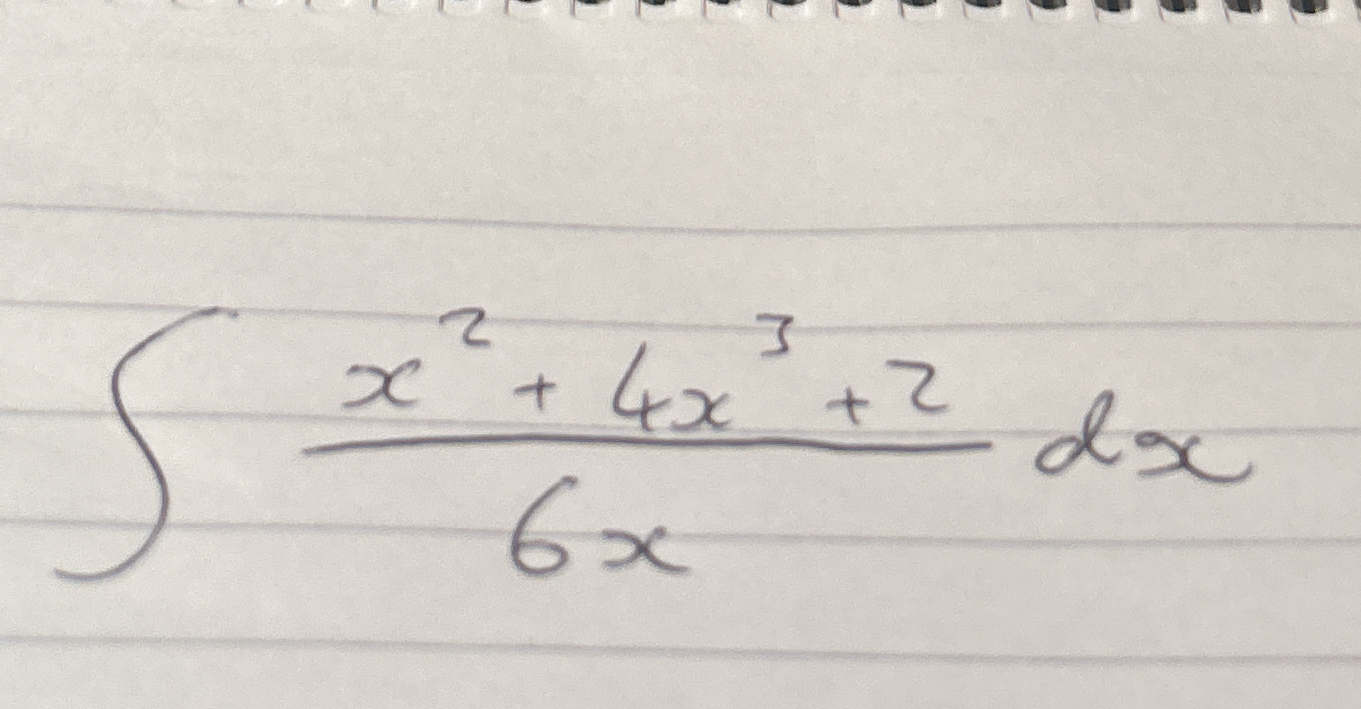
Understand the Problem
The question is asking for the evaluation of the integral of the given rational function. The high-level approach involves simplifying the integrand and then integrating term by term.
Answer
$$ \frac{x^2}{12} + \frac{2}{3}x + \frac{1}{3} \ln |x| + C $$
Answer for screen readers
The evaluated integral is:
$$ \frac{x^2}{12} + \frac{2}{3}x + \frac{1}{3} \ln |x| + C $$
Steps to Solve
- Rewrite the integrand
First, we simplify the integrand:
$$ \frac{x^2 + 4x + 2}{6x} = \frac{x^2}{6x} + \frac{4x}{6x} + \frac{2}{6x} = \frac{x}{6} + \frac{2}{3} + \frac{1}{3x} $$
- Set up the integral
Now, we set up the integral with the simplified terms:
$$ \int \left( \frac{x}{6} + \frac{2}{3} + \frac{1}{3x} \right) dx $$
- Integrate term by term
Next, we integrate each term separately:
$$ \int \frac{x}{6} dx = \frac{1}{6} \cdot \frac{x^2}{2} = \frac{x^2}{12} $$
$$ \int \frac{2}{3} dx = \frac{2}{3}x $$
$$ \int \frac{1}{3x} dx = \frac{1}{3} \ln |x| $$
- Combine the results
Combining all the integrated terms together gives:
$$ \int \frac{x^2 + 4x + 2}{6x} dx = \frac{x^2}{12} + \frac{2}{3}x + \frac{1}{3} \ln |x| + C $$
Where ( C ) is the constant of integration.
The evaluated integral is:
$$ \frac{x^2}{12} + \frac{2}{3}x + \frac{1}{3} \ln |x| + C $$
More Information
Integrating rational functions often involves breaking them down into simpler parts. The natural logarithm function arises when integrating terms like ( \frac{1}{x} ), which is a common occurrence in calculus.
Tips
- Neglecting the constant of integration: Always remember to add ( C ) after integrating.
- Forgetting to handle each term individually: Ensure to integrate each term separately and correctly simplify before integration.