Evaluate the integral of 1/(√x) dx.
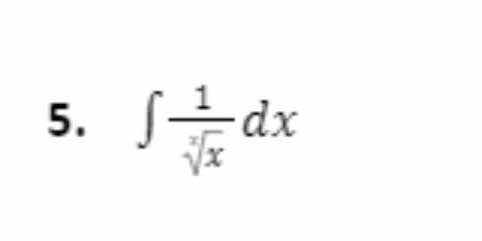
Understand the Problem
The question is asking to evaluate the integral of the function 1/(√x) with respect to x. This integral is related to basic calculus and will involve finding the antiderivative of the given expression.
Answer
The integral evaluates to $2\sqrt{x} + C$.
Answer for screen readers
The final answer is
$$ 2\sqrt{x} + C $$
Steps to Solve
- Rewrite the Integral
The given integral is
$$ \int \frac{1}{\sqrt{x}} , dx $$
We can rewrite $\frac{1}{\sqrt{x}}$ as $x^{-1/2}$.
- Apply the Power Rule for Integration
Using the power rule of integration, which states that
$$ \int x^n , dx = \frac{x^{n+1}}{n+1} + C $$
for $n \neq -1$, we set $n = -\frac{1}{2}$. Thus, we have:
$$ \int x^{-1/2} , dx = \frac{x^{\frac{1}{2}}}{\frac{1}{2}} + C $$
- Simplify the Expression
Simplifying the expression from the previous step gives:
$$ \frac{x^{\frac{1}{2}}}{\frac{1}{2}} = 2x^{\frac{1}{2}} $$
So we have:
$$ \int \frac{1}{\sqrt{x}} , dx = 2\sqrt{x} + C $$
The final answer is
$$ 2\sqrt{x} + C $$
More Information
This integral represents the area under the curve of the function $f(x) = \frac{1}{\sqrt{x}}$. The constant $C$ denotes the constant of integration, which is included because the integral represents a family of functions.
Tips
- Forgetting to add the constant of integration $C$ after evaluating the integral.
- Misapplying the power rule by incorrectly adding or altering the exponent.
AI-generated content may contain errors. Please verify critical information