Evaluate the integral of 1/(ln(x) * x^6) dx.
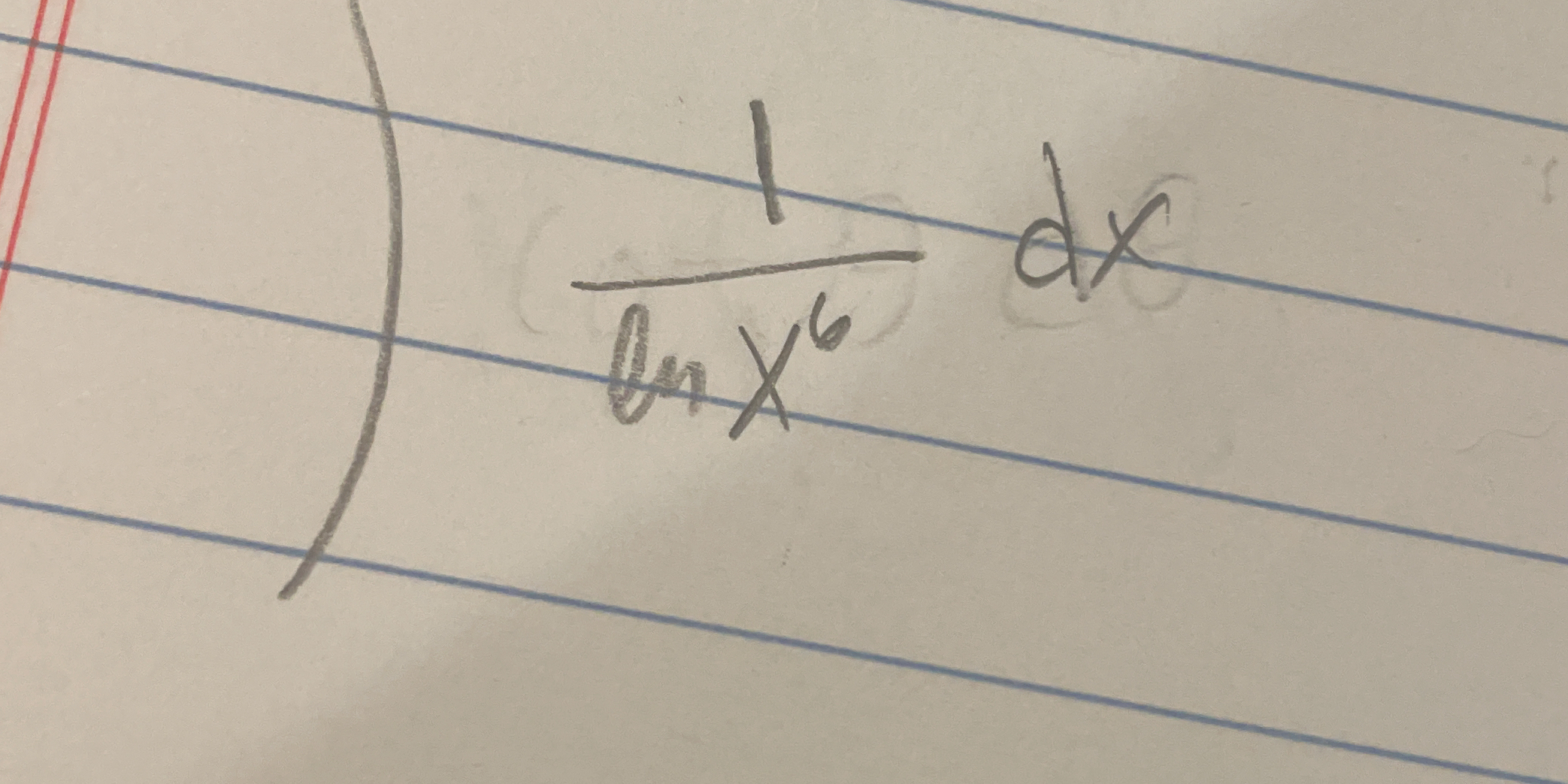
Understand the Problem
The question appears to be asking for the integration of the function 1/(ln(x) * x^6) with respect to x. The user is likely looking for guidance on solving this integral.
Answer
$$ I = -\text{Ei}(-5 \ln(x)) + C $$
Answer for screen readers
The integral is given by: $$ I = -\text{Ei}(-5 \ln(x)) + C $$
Steps to Solve
-
Identify the Integral We need to solve the integral: $$ I = \int \frac{1}{\ln(x) \cdot x^6} , dx $$
-
Substitution To simplify this integral, we can use the substitution: $$ u = \ln(x) $$ Then, the derivative is: $$ du = \frac{1}{x} , dx \implies dx = x , du = e^u , du $$
Substituting $x = e^u$ gives us: $$ I = \int \frac{1}{u \cdot (e^u)^6} \cdot e^u , du = \int \frac{e^{-5u}}{u} , du $$
-
Rewrite the Integral Now we rewrite the integral in terms of $u$: $$ I = \int \frac{e^{-5u}}{u} , du $$
-
Integral Representation The integral $\int \frac{e^{-5u}}{u} , du$ does not have a simple form and is represented using the Exponential Integral function, denoted as: $$ \text{Ei}(x) $$
-
Final Expression Thus, the final solution for the integral is: $$ I = -\text{Ei}(-5 \ln(x)) + C $$ where $C$ is the constant of integration.
The integral is given by: $$ I = -\text{Ei}(-5 \ln(x)) + C $$
More Information
The Exponential Integral function $\text{Ei}(x)$ is a special function that cannot generally be expressed in elementary functions. This function arises frequently in problems involving integrals that involve logarithmic and exponential terms.
Tips
- Confusing the limits of integration: Ensure to understand if the integral is definite or indefinite.
- Incorrectly substituting or differentiating: Be careful with how the substitution affects the limits and bounds, especially if it is a definite integral.
AI-generated content may contain errors. Please verify critical information