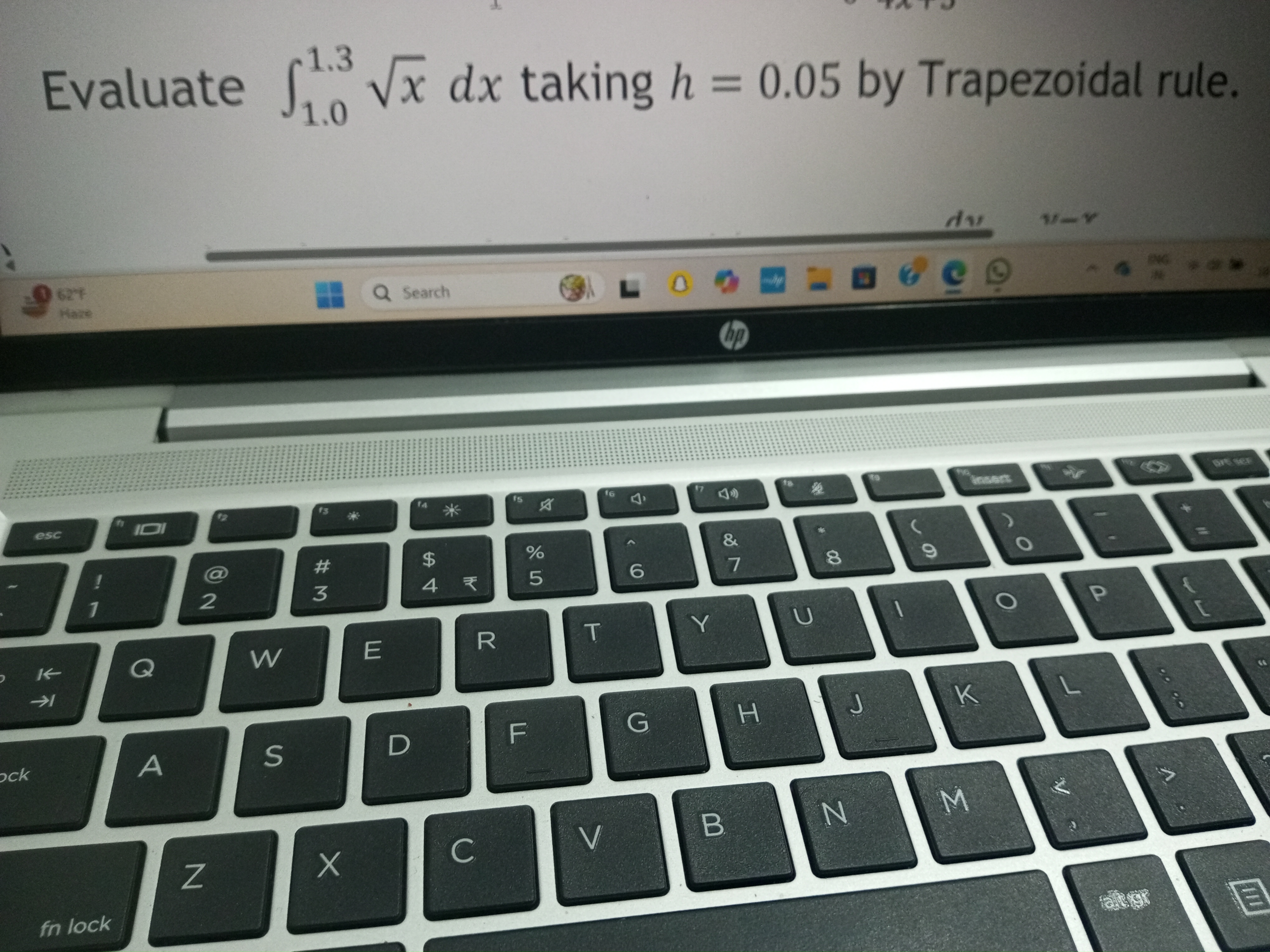
Evaluate the integral from 1.0 to 1.3 of sqrt(x) dx taking h = 0.05 by Trapezoidal rule.
Understand the Problem
The question is asking to evaluate the definite integral of the function √x from 1.0 to 1.3 using the Trapezoidal rule with a given interval width of h = 0.05. This involves applying the numerical method of integration to approximate the area under the curve of the function over the specified interval.
Answer
The approximate value of the integral is \( 0.3053 \).
Answer for screen readers
The approximate value of the integral ( \int_{1.0}^{1.3} \sqrt{x} , dx ) using the Trapezoidal rule with ( h = 0.05 ) is approximately ( 0.3053 ).
Steps to Solve
- Determine the number of intervals (n)
The width of each interval is given by ( h = 0.05 ). To find the number of intervals ( n ), use the formula: $$ n = \frac{b - a}{h} $$ where ( a = 1.0 ) and ( b = 1.3 ): $$ n = \frac{1.3 - 1.0}{0.05} = \frac{0.3}{0.05} = 6 $$
- Calculate the x-values
The x-values at each interval can be calculated as:
- ( x_0 = 1.0 )
- ( x_1 = x_0 + h = 1.0 + 0.05 = 1.05 )
- ( x_2 = x_1 + h = 1.05 + 0.05 = 1.10 )
- ( x_3 = x_2 + h = 1.10 + 0.05 = 1.15 )
- ( x_4 = x_3 + h = 1.15 + 0.05 = 1.20 )
- ( x_5 = x_4 + h = 1.20 + 0.05 = 1.25 )
- ( x_6 = x_5 + h = 1.25 + 0.05 = 1.30 )
- Calculate the function values
Now compute ( f(x) = \sqrt{x} ) at each x-value:
- ( f(x_0) = \sqrt{1.0} = 1.0 )
- ( f(x_1) = \sqrt{1.05} \approx 1.0247 )
- ( f(x_2) = \sqrt{1.10} \approx 1.0488 )
- ( f(x_3) = \sqrt{1.15} \approx 1.2247 )
- ( f(x_4) = \sqrt{1.20} \approx 1.0954 )
- ( f(x_5) = \sqrt{1.25} = 1.118 )
- ( f(x_6) = \sqrt{1.30} \approx 1.1402 )
- Apply the Trapezoidal Rule formula
The Trapezoidal Rule formula for approximating the integral is given by: $$ \int_a^b f(x) , dx \approx \frac{h}{2} \left( f(x_0) + 2f(x_1) + 2f(x_2) + 2f(x_3) + 2f(x_4) + 2f(x_5) + f(x_6) \right) $$
Substituting the function values: $$ I \approx \frac{0.05}{2} \left( 1.0 + 2(1.0247) + 2(1.0488) + 2(1.2247) + 2(1.0954) + 2(1.118) + 1.1402 \right) $$
- Calculate the integral
Now performing the calculations step-by-step:
- Sum of function values: $$ 1.0 + 2(1.0247) + 2(1.0488) + 2(1.2247) + 2(1.0954) + 2(1.118) + 1.1402 $$ Calculating yields: $$ = 1.0 + 2.0494 + 2.0976 + 2.4494 + 2.1908 + 2.236 + 1.1402 = 12.2134 $$
Final approximation: $$ I \approx \frac{0.05}{2} \times 12.2134 = 0.025 \times 12.2134 = 0.305335 $$
The approximate value of the integral ( \int_{1.0}^{1.3} \sqrt{x} , dx ) using the Trapezoidal rule with ( h = 0.05 ) is approximately ( 0.3053 ).
More Information
The Trapezoidal rule is a method of numerical integration that approximates the area under a curve by dividing it into trapezoids rather than rectangles. This method provides a better approximation than methods that use rectangular areas, especially for curves that are relatively linear over small intervals.
Tips
- Incorrect interval calculation: Make sure to carefully compute the number of intervals using the formula ( n = \frac{b - a}{h} ).
- Miscalculating function values: Errors can occur in computing ( f(x) = \sqrt{x} ) for each x-value, so ensure proper evaluation.
- Forgetting the coefficients in the formula: Remember to apply the factor of ( \frac{h}{2} ) and recognize which function values are multiplied by 2.
AI-generated content may contain errors. Please verify critical information