(3x - 1)² - (x + 6)²
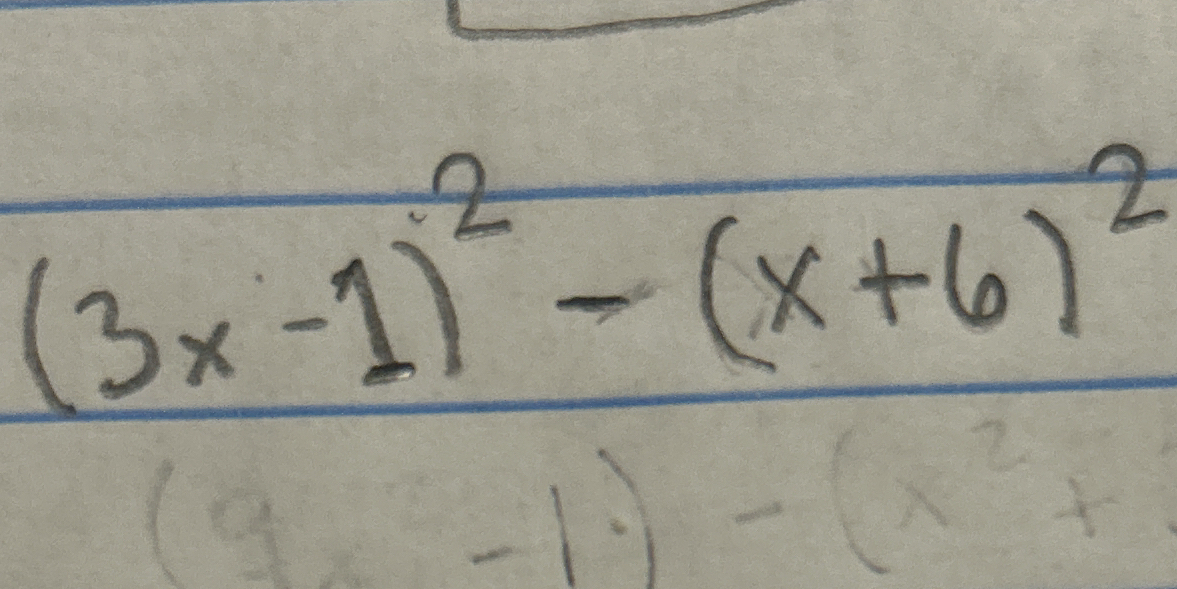
Understand the Problem
The question provides an expression involving the squares of two binomials and indicates a subtraction operation between them. It requires evaluating or simplifying the expression.
Answer
The simplified expression is \(8x^2 - 18x - 35\).
Answer for screen readers
The simplified expression is (8x^2 - 18x - 35).
Steps to Solve
- Expand the First Binomial Square
Use the formula $(a - b)^2 = a^2 - 2ab + b^2$, where $a = 3x$ and $b = 1$. [ (3x - 1)^2 = (3x)^2 - 2(3x)(1) + (1)^2 = 9x^2 - 6x + 1 ]
- Expand the Second Binomial Square
Using the same formula $(a + b)^2 = a^2 + 2ab + b^2$, where $a = x$ and $b = 6$. [ (x + 6)^2 = (x)^2 + 2(x)(6) + (6)^2 = x^2 + 12x + 36 ]
- Substitute the Expansions into the Original Expression
Now, replace the squared terms in the original expression: [ (3x - 1)^2 - (x + 6)^2 = (9x^2 - 6x + 1) - (x^2 + 12x + 36) ]
- Distribute the Negative Sign
Distributing the negative sign across the second expanded binomial: [ = 9x^2 - 6x + 1 - x^2 - 12x - 36 ]
- Combine Like Terms
Now, combine the like terms: [ (9x^2 - x^2) + (-6x - 12x) + (1 - 36) = 8x^2 - 18x - 35 ]
The simplified expression is (8x^2 - 18x - 35).
More Information
This expression represents a quadratic polynomial resulting from the subtraction of the squared binomials. Quadratic expressions can often be factored or analyzed for roots using the quadratic formula.
Tips
- Forgetting to distribute the negative sign correctly when subtracting the second binomial square.
- Incorrectly combining like terms, leading to errors in the final polynomial.
AI-generated content may contain errors. Please verify critical information